| Classe | Absoluta | Relativa (%) | Absoluta | Relativa (%) |
|---|---|---|---|---|
| 0+ — 20 | 10 | 20 | 10 | 20 |
| 20+ — 40 | 18 | 36 | 28 | 56 |
| 40+ — 60 | 11 | 22 | 39 | 78 |
| 60+ — 80 | 6 | 12 | 45 | 90 |
| 80+ — 100 | 4 | 8 | 49 | 98 |
| 100+ — 120 | 1 | 2 | 50 | 100 |
| Total | 50 | 100 |
4 Dados Quantitativos
Quando a variável a descrever é de natureza quantitativa o campo de possibilidades de análise é muito maior.
Esta secção começa por discutir a organização dos dados. Segue-se depois a apresentação das formas mais comuns de representação gráfica e o cálculo e interpretação de estatísticas numéricas.
4.1 Organização dos dados
Antes de avançar para os métodos propriamente ditos, é necessário considerar como os dados estão organizados e, em caso de necessidade, organizar os mesmos.
Há três possibilidades para a organização dos dados: dados desagrupados, dados discretos agrupados e dados contínuos agrupados.
4.1.1 Dados desagrupados
Quando se diz que os dados estão desagrupados, significa que ainda não sofreram qualquer tratamento, ou seja, são os dados em bruto, tal como recolhidos, possivelmente depois de serem corrigidas eventuais inconsistências. Por exemplo, o conjunto de dados cars apresenta a variável dist com distância de paragem para um conjunto de carros (em pés ou feet, 1 ft = 30.48 cm). Estes dados estão desagrupados:
2, 10, 4, 22, 16, 10, 18, 26, 34, 17, 28, 14, 20, 24, 28, 26, 34, 34, 46, 26, 36, 60, 80, 20, 26, 54, 32, 40, 32, 40, 50, 42, 56, 76, 84, 36, 46, 68, 32, 48, 52, 56, 64, 66, 54, 70, 92, 93, 120, 85
Quando se faz análise no computador, o ideal é ter os dados o menos tratados possível, na forma de dados desagrupados. É sempre possível agrupar os dados mas, nem sempre é possível desagrupar, uma vez que, ao agrupar, pode ser perdida informação.
4.1.2 Dados contínuos agrupados
Os dados desagrupados apresentados acima são difíceis de apreender, pois trata-se de uma lista de números com alguma extensão. A forma mais comum de sumariar os dados é construir uma tabela de frequências, vagamente semelhantes às tabelas de contingência apresentadas na Secção 3.1.
Numa tabela de frequências o intervalo de valores que a variável abrange é dividido em sub-intervalos, denominados por células ou classes utilizando um critério apropriado, dependente do objetivo. Por exemplo, poder-se-iam resumir as distâncias de paragem numa tabela semelhante à Tabela 4.1.
Na Tabela 4.1, para lá das frequências absolutas e relativas (\(f_k\) e \(f'_k\)), apresentam-se ainda as frequências acumuladas absolutas e relativas (\(F_k\) e \(F'_k\)). As frequências acumuladas permitem ter a noção de quais os conjunto de células com frequências importantes ou insignificantes.
Se \(f_k\) representar a frequência absoluta da classe \(k\) e \(n\) for o total de observações, ou seja, \(n=\sum_k f_k\), então:
Freqência relativa: \(f'_k = \frac{f_k}{n}\)
Frequência absoluta acumulada: \(F_k = \sum_{i=1}^{k}f_i\)
Frequência relativa acumulada: \(F'_k = \sum_{i=1}^{k}f'_i = \frac{F_k}{n}\)
Note-se que foram tomadas várias decisões, mais ou menos arbitrárias, na construção da tabela de frequências:
- Número de células: \(K=\) 6.
- Células iguais com uma amplitude \(a_k=\) 20 unidades.
- Limite inferior da primeira célula: 0.
- Limite superior da última célula: 120.
- Limite superior fechado (inclui valores iguais ao limite).
Desta forma, as células abrangem desde o mínimo (2) até ao máximo (120). Naturalmente, desde que as células incluam todas as observações, podem ser definidas arbitrariamente, podendo ter amplitudes iguais ou diferentes (pouco usual). Voltar-se-á a este assunto mais à frente.
Ao agrupar os dados, é perdida informação. Se apenas se conhecer a tabela de frequências, é impossível reconstituir os dados originais, apenas os podemos aproximar.
4.1.3 Dados discretos agrupados
Quando os dados são de natureza discreta ou são dados contínuos que sofreram arredondamento, podemos agrupar os dados sem perder informação. Os dados a seguir (gerados ao acaso) representam as idades dos alunos de uma turma com 35 alunos.
21, 20, 20, 19, 22, 20, 21, 20, 20, 19, 17, 22, 20, 22, 23, 21, 23, 19, 22, 19, 20, 19, 19, 18, 20, 23, 20, 22, 19, 20, 20, 20, 23, 19, 20
Os dados poderiam ser sumariados com uma tabela semelhante à Tabela 4.2.
| Idade | Absoluta | Relativa (%) | Absoluta | Relativa (%) |
|---|---|---|---|---|
| 17 | 1 | 2.9 | 1 | 2.9 |
| 18 | 1 | 2.9 | 2 | 5.7 |
| 19 | 8 | 22.9 | 10 | 28.6 |
| 20 | 13 | 37.1 | 23 | 65.7 |
| 21 | 3 | 8.6 | 26 | 74.3 |
| 22 | 5 | 14.3 | 31 | 88.6 |
| 23 | 4 | 11.4 | 35 | 100.0 |
| Total | 35 | 100.0 |
A diferença para os dados contínuos está na existência de um conjunto restrito de valores discretos. Para construir a tabela de frequências, em vez de definir células como anteriormente, neste caso, cada célula corresponde a um dos valores.
Note-se que estes tipo de dados tem semelhanças com as variáveis ordinais, no sentido em que se trata de um conjunto de valores ordenados. De facto, a forma mais assertiva de representar graficamente esta informação, seria através de um gráfico de barras como o da Figura 4.1.
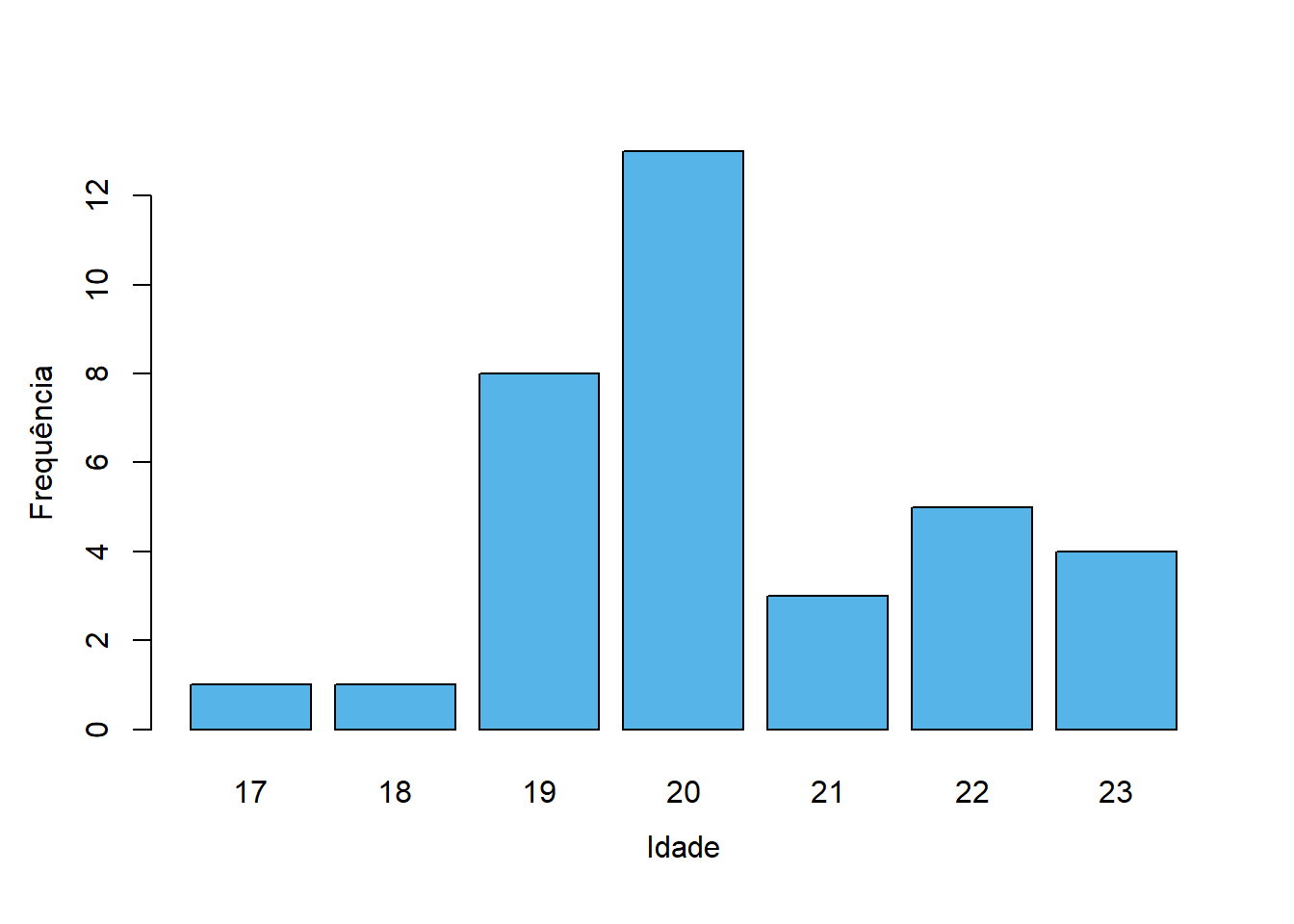
Quando se agrupam dados discretos desta forma, não há perda de informação (exceto a ordem das observações, caso fosse relevante). É equivalente ter dados desagrupados ou agrupados desta forma.
Para não sobrecarregar este texto, considera-se que temos à disposição dados desagrupados. Quando se está perante dados agrupados em classes, como na Secção 4.1.2 ou na Secção 4.1.3, eventualmente provenientes de uma fonte secundária, há expressões para calcular diversas estatísticas a partir da tabela de frequências que podem ser obtidas de qualquer bom livro de estatística, como Guimarães & Cabral (2010), por exemplo.
4.2 Representação de frequências
Quando se está perante dados desagrupados, um procedimento exploratório comum é a construção de uma tabela de frequências e sua representação gráfica. A forma mais comum de o fazer é através de um histograma.
À semelhança do gráfico de barras, o histograma representa cada classe com uma barra, cuja altura é proporcional à frequência da classe. A figura Figura 4.2 representa graficamente a Tabela 4.1, que contém as frequências das distâncias de paragem de um conjunto de carros.
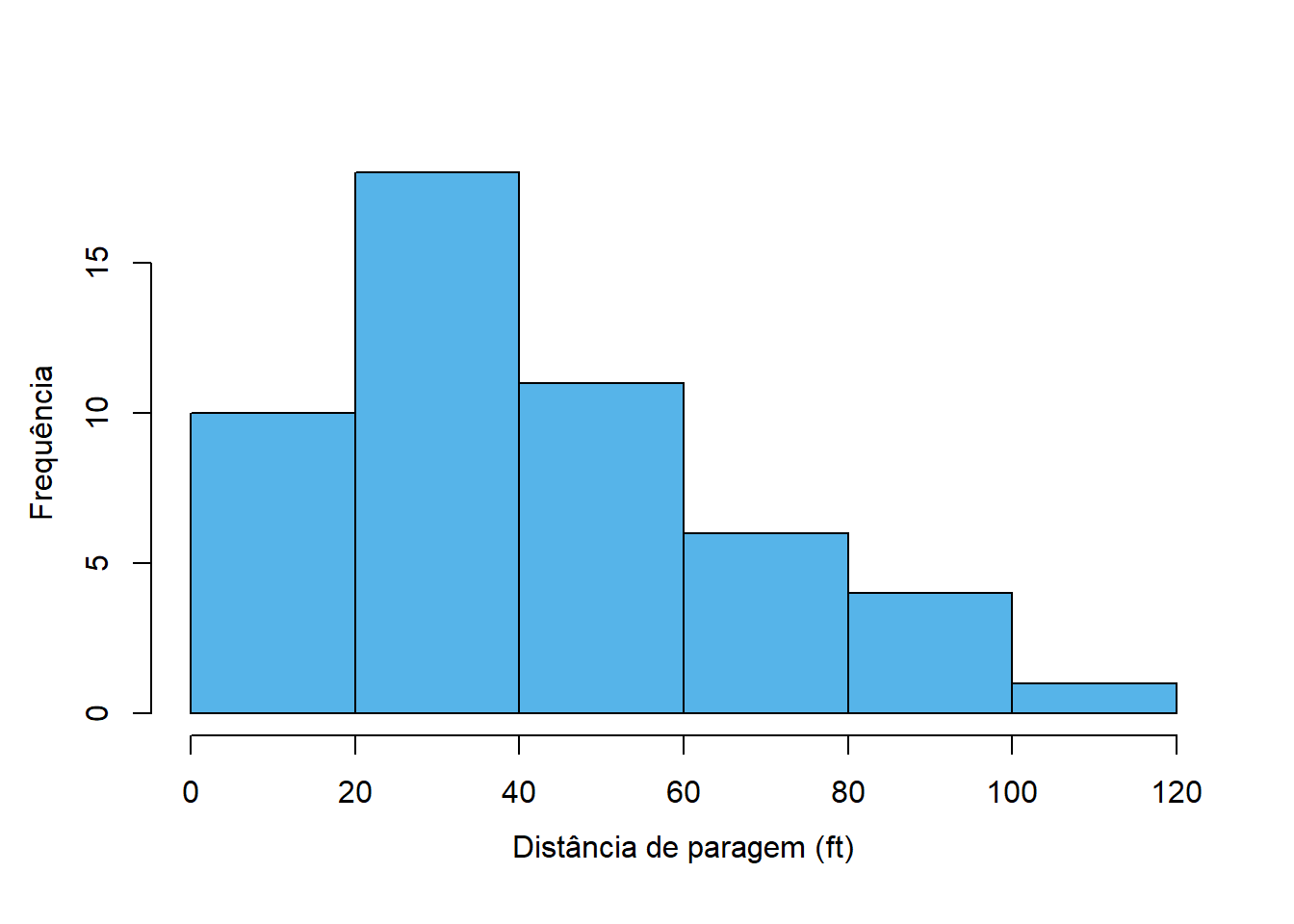
Note-se que há diferenças muito importantes para o gráfico de barras:
- O eixo horizontal é numérico, no gráfico de barras eram categorias.
- Não há separação entre as barras, o que reforça a ideia de continuidade.
4.2.1 Definição das classes
Para elaborar um histograma é necessário decidir o número de classes, \(K\), a amplitude de cada classe, \(a_k\), e onde se localiza cada classe (limites inferior e superior).
A decisão mais importante é o número de classes. O histograma deve ter um número de classes equilibrado tendo em atenção o seguinte:
- Um número de classes muito pequeno produz uma visualização pouco informativa.
- Um número de classes muito grande produz uma visualização confusa com demasiados detalhes irrelevantes.
A Figura 4.3 mostra algumas variantes ao histograma apresentado anteriormente para ilustrar esta questão. Na variante 4.3 (a) o número de classes é claramente escasso e a análise do gráfico não fornece grande informação. Já na variante 4.3 (d) o número de classes é claramente exagerado, havendo muitas classes com uma ou nenhuma observação e demasiados detalhes que dificultam a análise.
As figuras 4.3 (b), 4.3 (c), 4.3 (d) e 4.3 (e) implementam diversos métodos conhecidos para determinar o número de classes e produzem resultados aceitáveis.
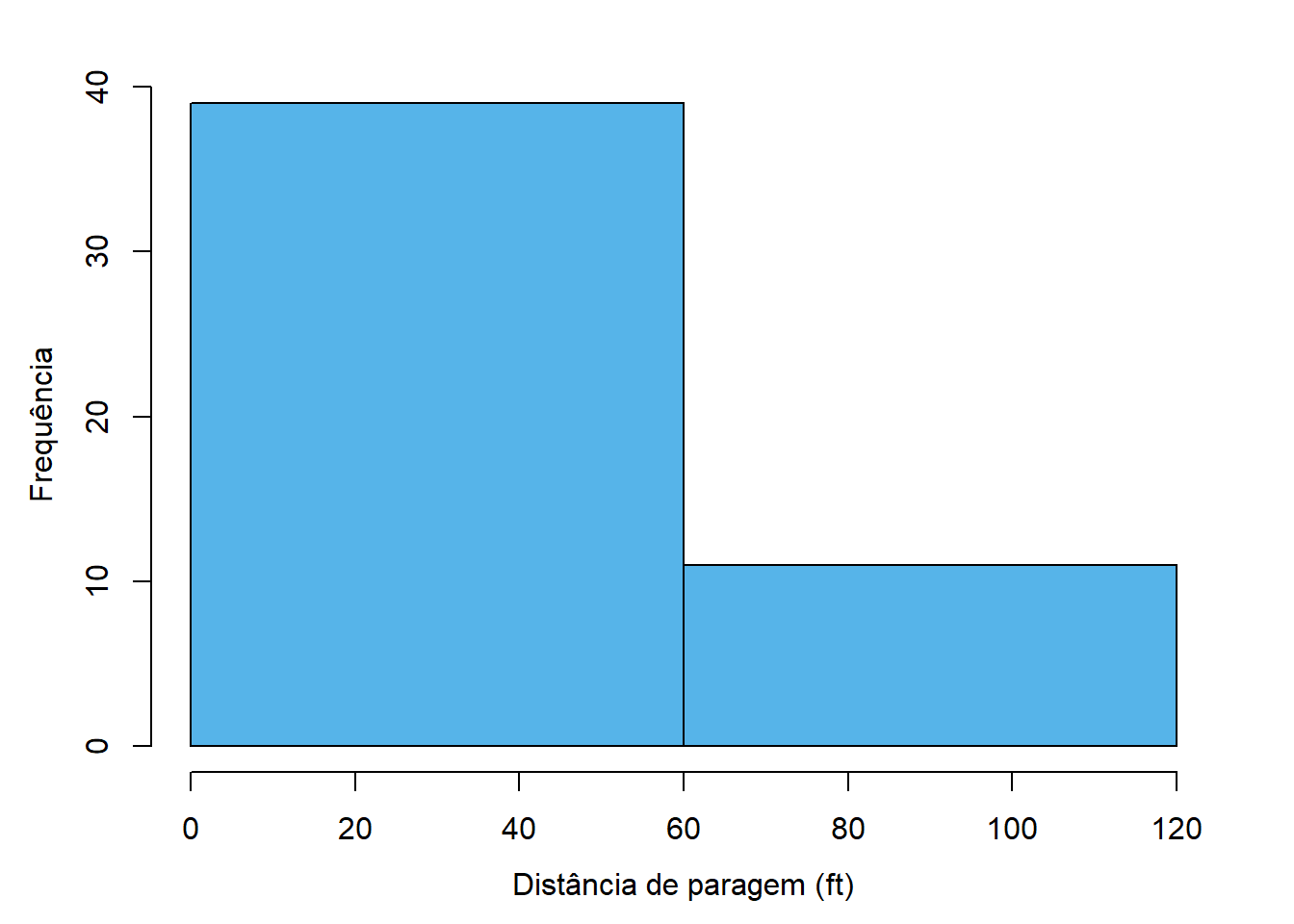
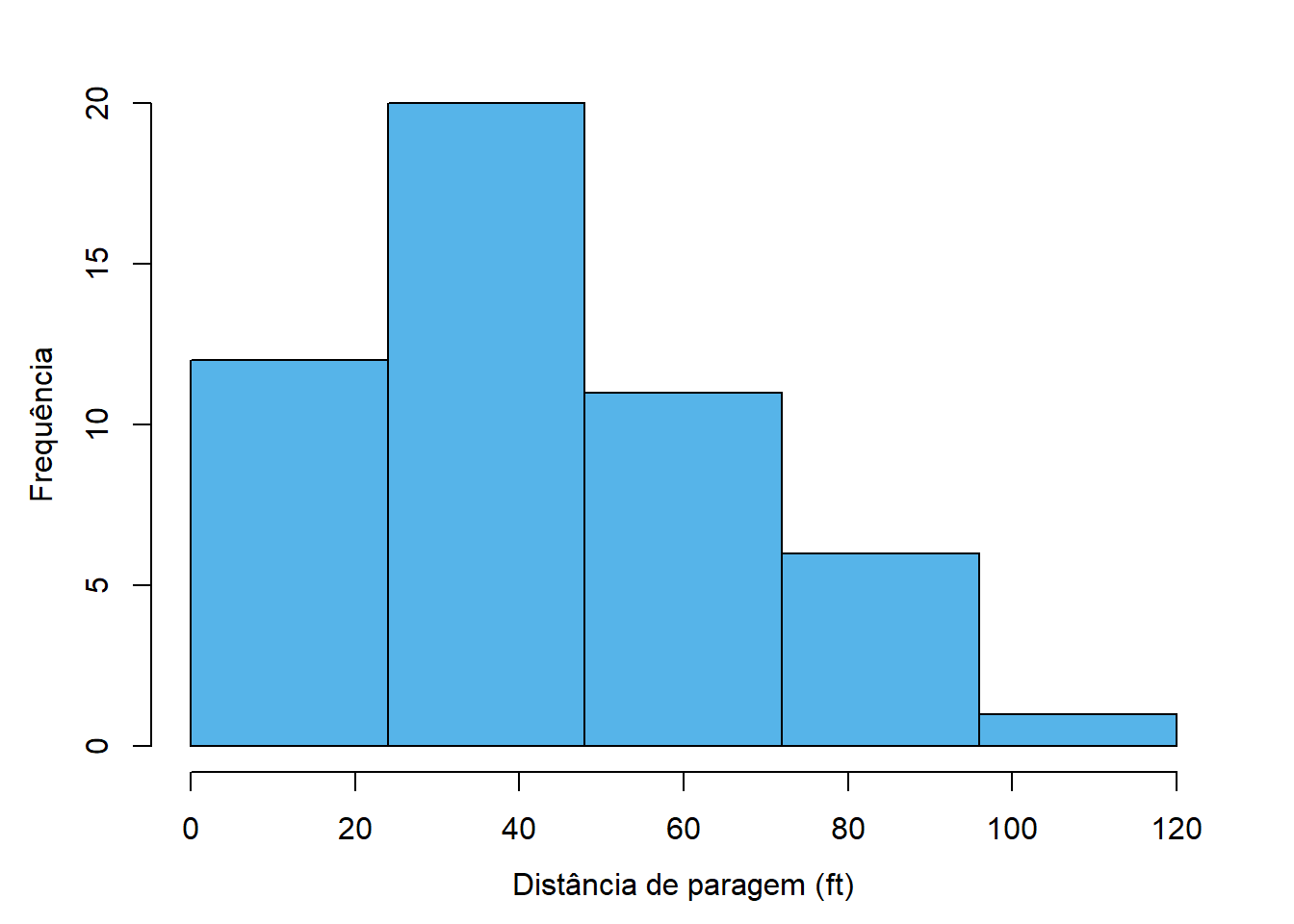
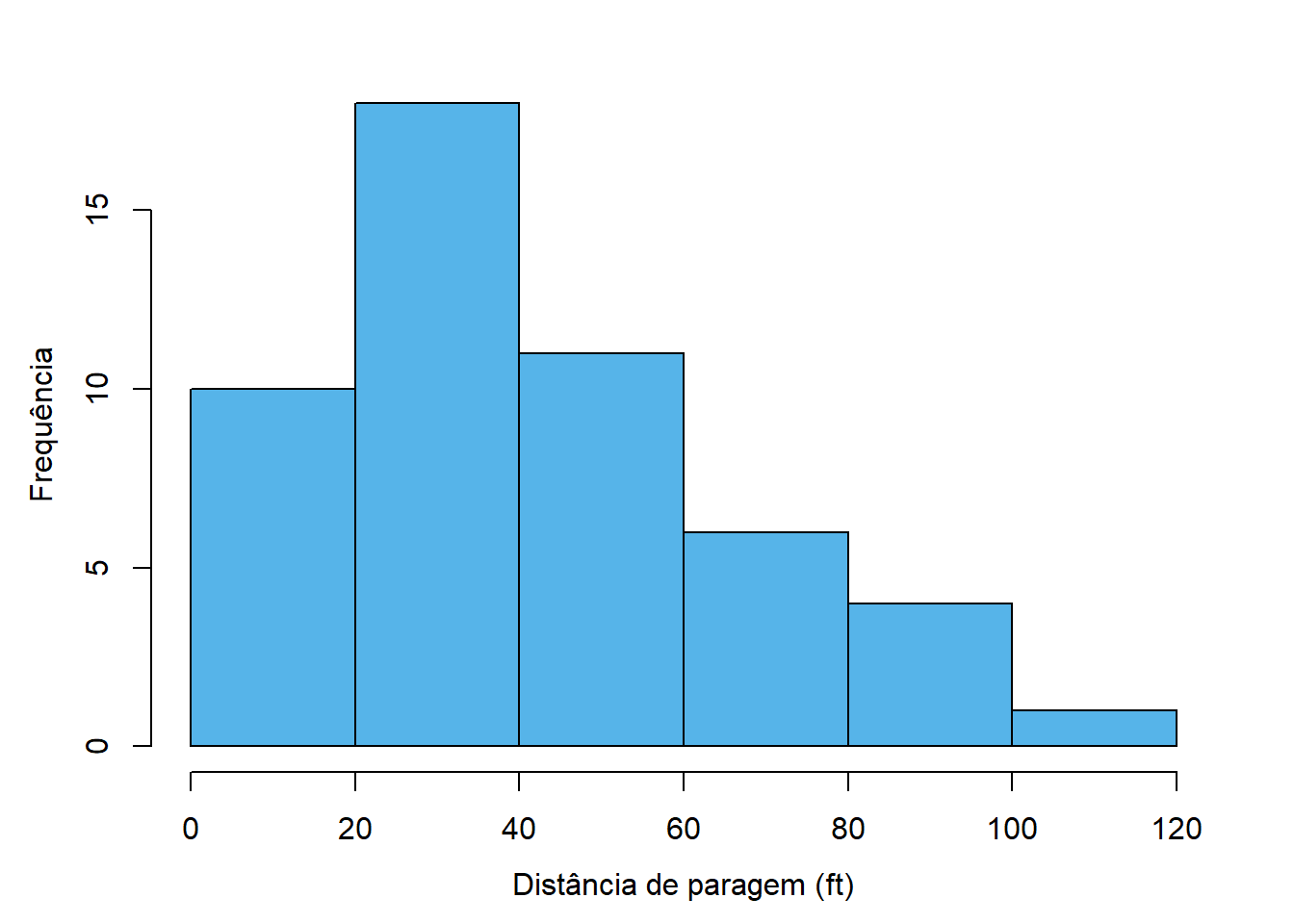
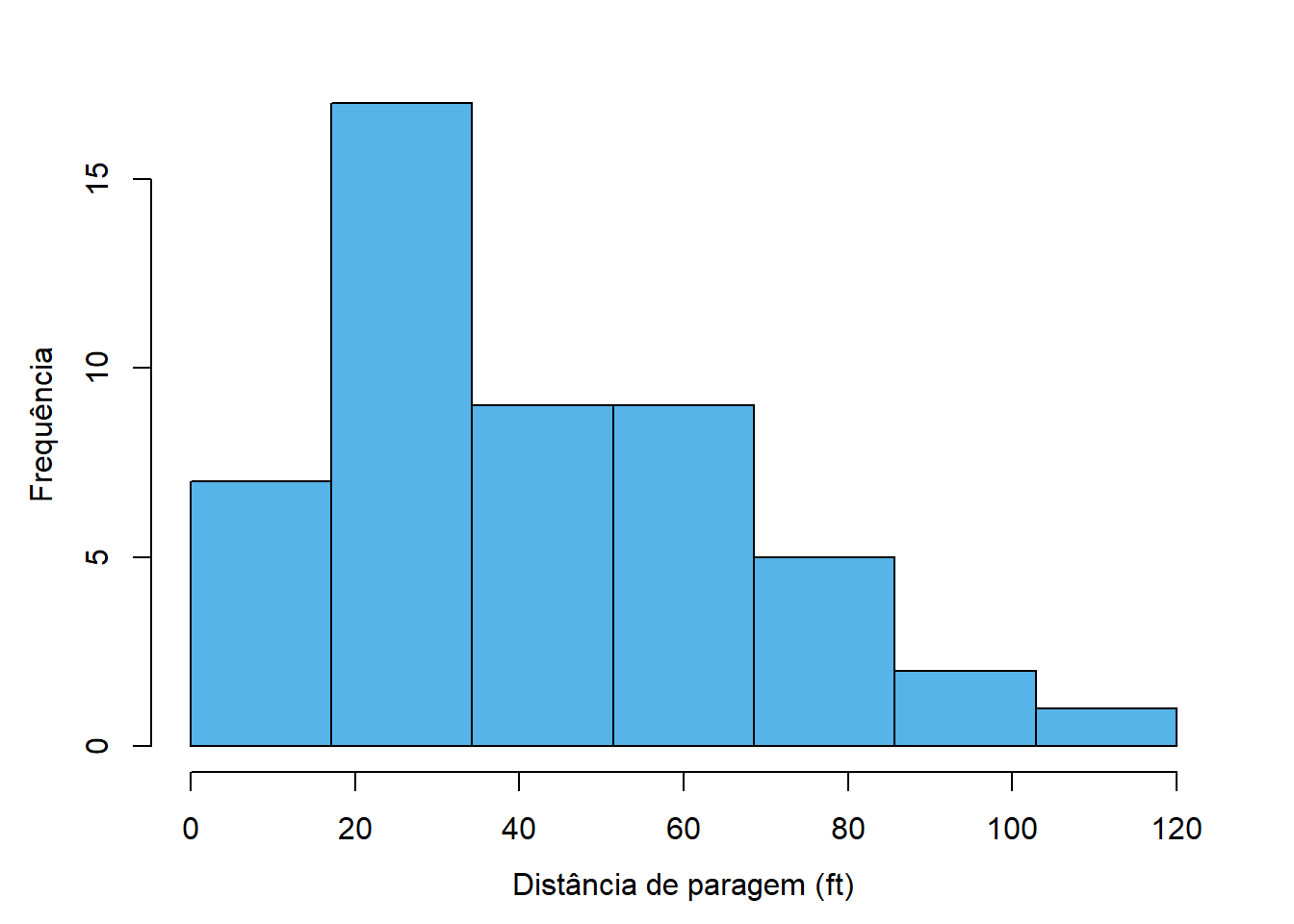
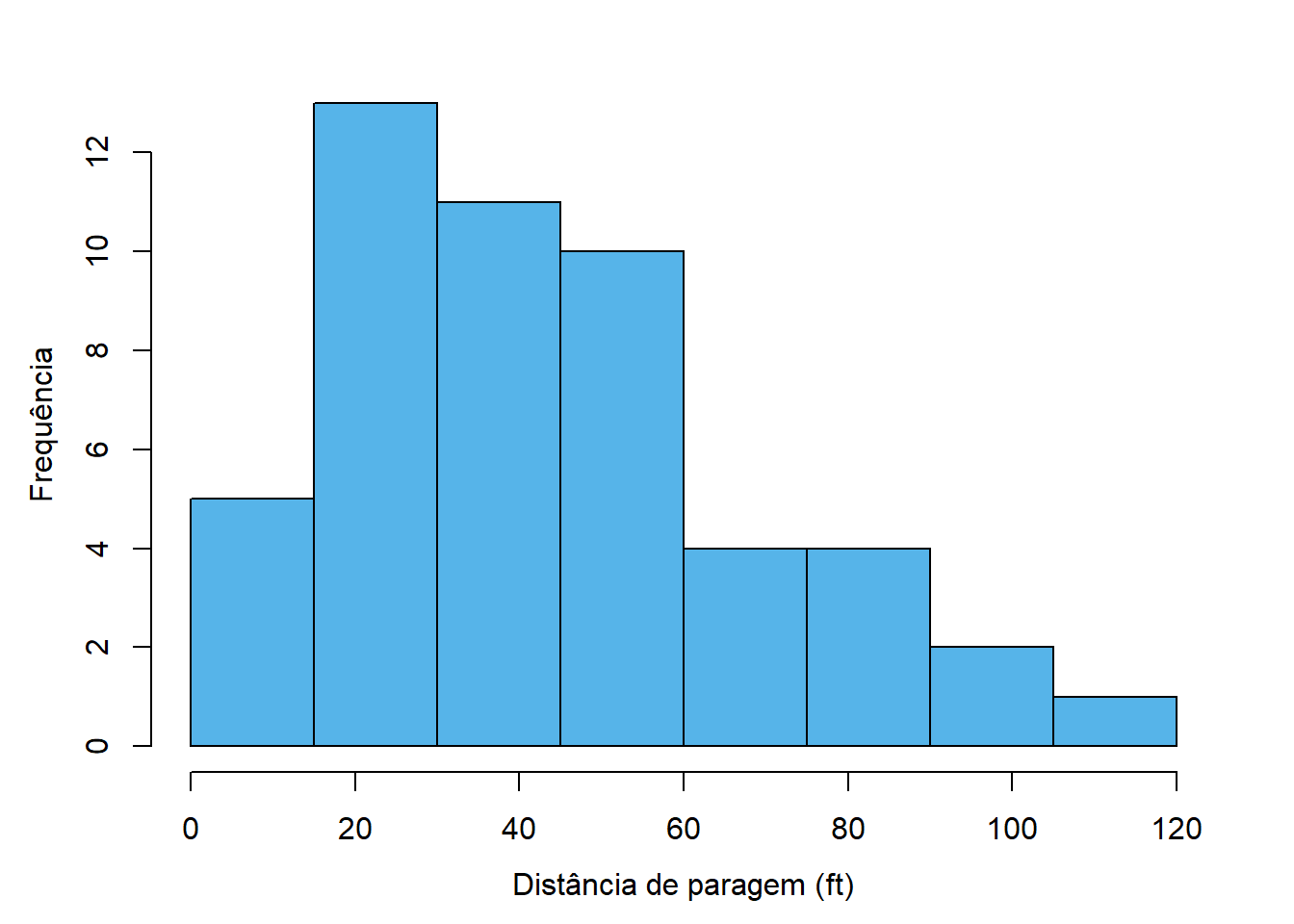
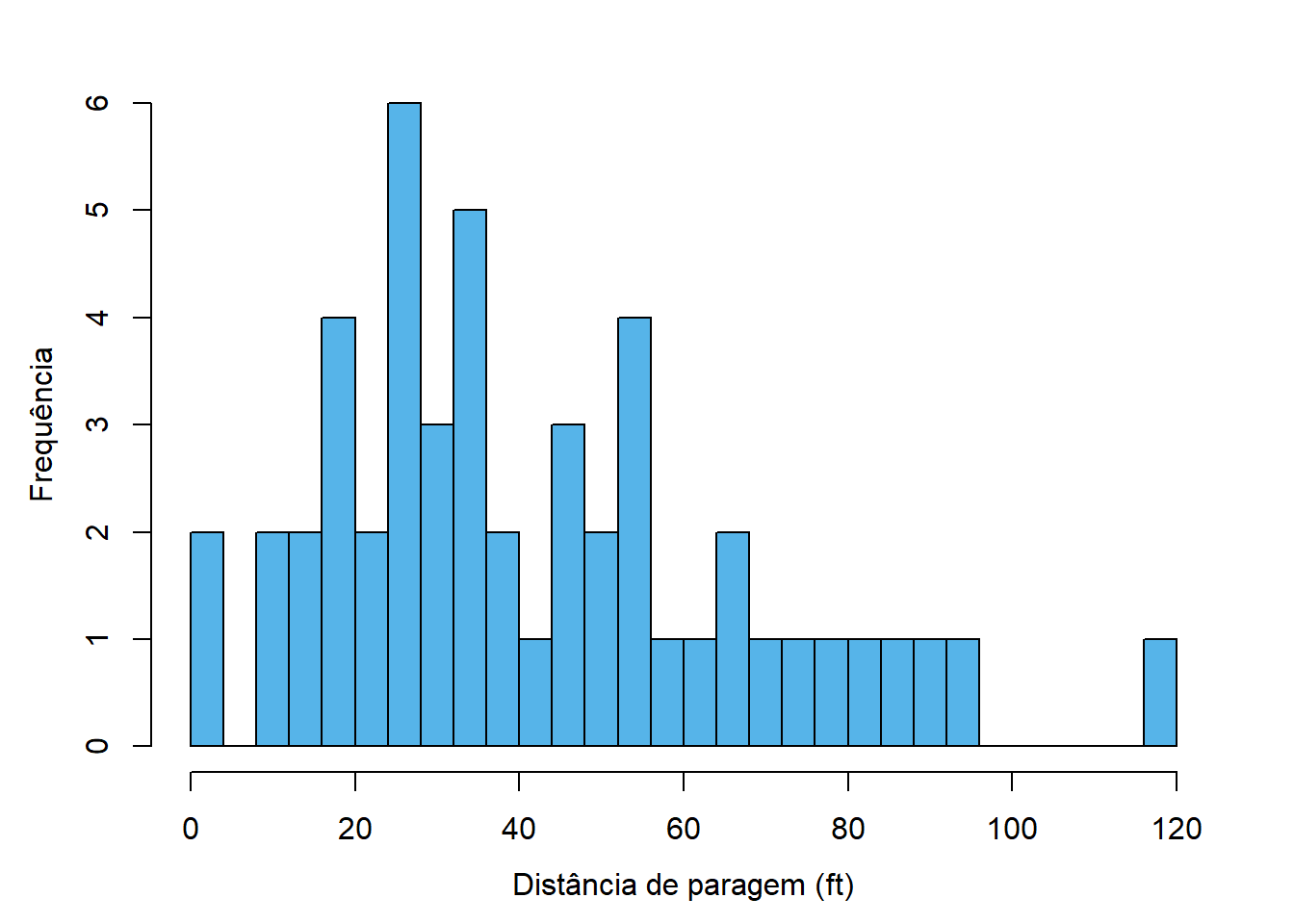
Em todos os casos, o limite inferior da primeira classe é 0 (em vez do mínimo, que é 2) e o limite superior é 120 (que coincide com o máximo). Esta estratégia produz resultados esteticamente mais agradáveis e permite julgar mais facilmente os limites das classes.
O R tenta sempre alinhar os limites das classes com os intervalos do eixo horizontal, alterando ligeiramente o número de classes recomendado pelos vários métodos que implementa (Sturges (por omissão), Scott e Freedman-Diaconis) para fazer aquele alinhamento. Trata-se de promover um equilíbrio entre questões teóricas, questões práticas e questões estéticas, sempre importantes na visualização de dados.
4.2.2 Análise do histograma
Um histograma permite uma perspetiva rápida sobre a forma como os dados estão distribuídos, sendo muito bom para julgar 3 aspetos: o tipo de moda, a simetria e a presença de observações incomuns.
Tipo de moda
Em estatística, a moda é o valor (ou vizinhança de um valor) onde a concentração (densidade) de observações é máxima. Perante dados discretos é fácil de determinar a moda, bastando verificar qual o valor mais frequente. No caso de dados contínuos é necessário fazer uma estimativa por outros métodos, uma vez que, por definição, a ocorrência de valores iguais é improvável, ocorrendo quase sempre devido ao arredondamento das medições.
Como a determinação de uma estimativa exata da moda tem um interesse limitado, o histograma pode ser utilizado para ter uma ideia do tipo de moda que os dados apresentam. Desta forma, são de notar 4 casos:
Distribuição unimodal: tal como o nome indica, há apenas uma moda, ou seja, o histograma apresenta um único pico proeminente, sendo o caso da Figura 4.4 (a). É uma das situações mais frequentes.
Distribuição bimodal: neste caso já há duas modas, ou seja, o histograma apresenta dois picos proeminentes, sendo o caso da Figura 4.4 (b).
Distribuição multimodal: trata-se de uma generalização dos conceitos anteriores às situações em que há mais do que dois dois picos proeminentes no histograma, sendo o caso da Figura 4.4 (c). O facto de haver mais do que uma moda levanta a questão da causa, que pode dever-se a uma qualquer característica dos dados com interesse.
Distribuição uniforme: neste caso não é possível identificar qualquer pico proeminente, tendo todas as barras do histograma uma altura semelhante, como no caso da Figura 4.4 (d).
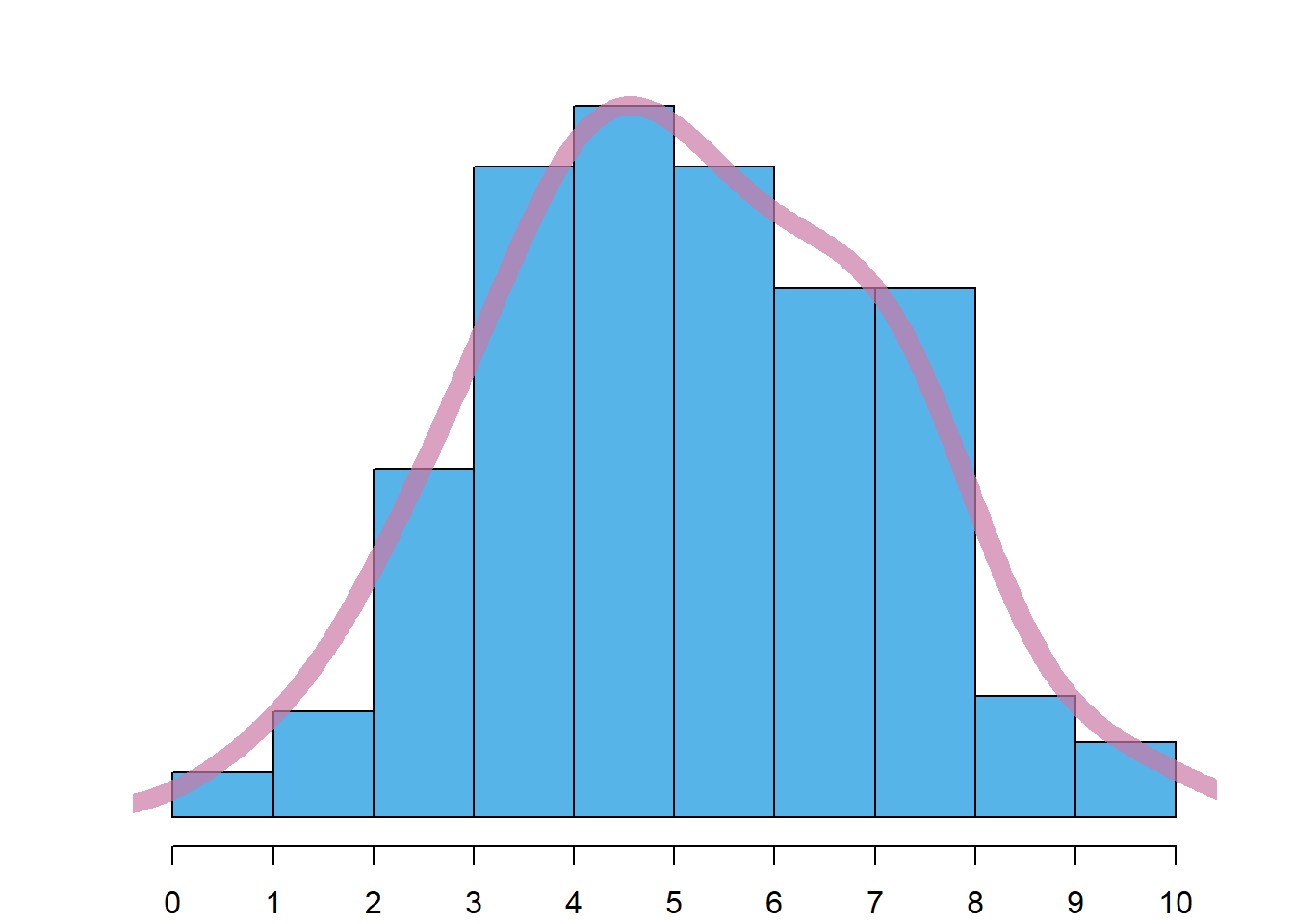
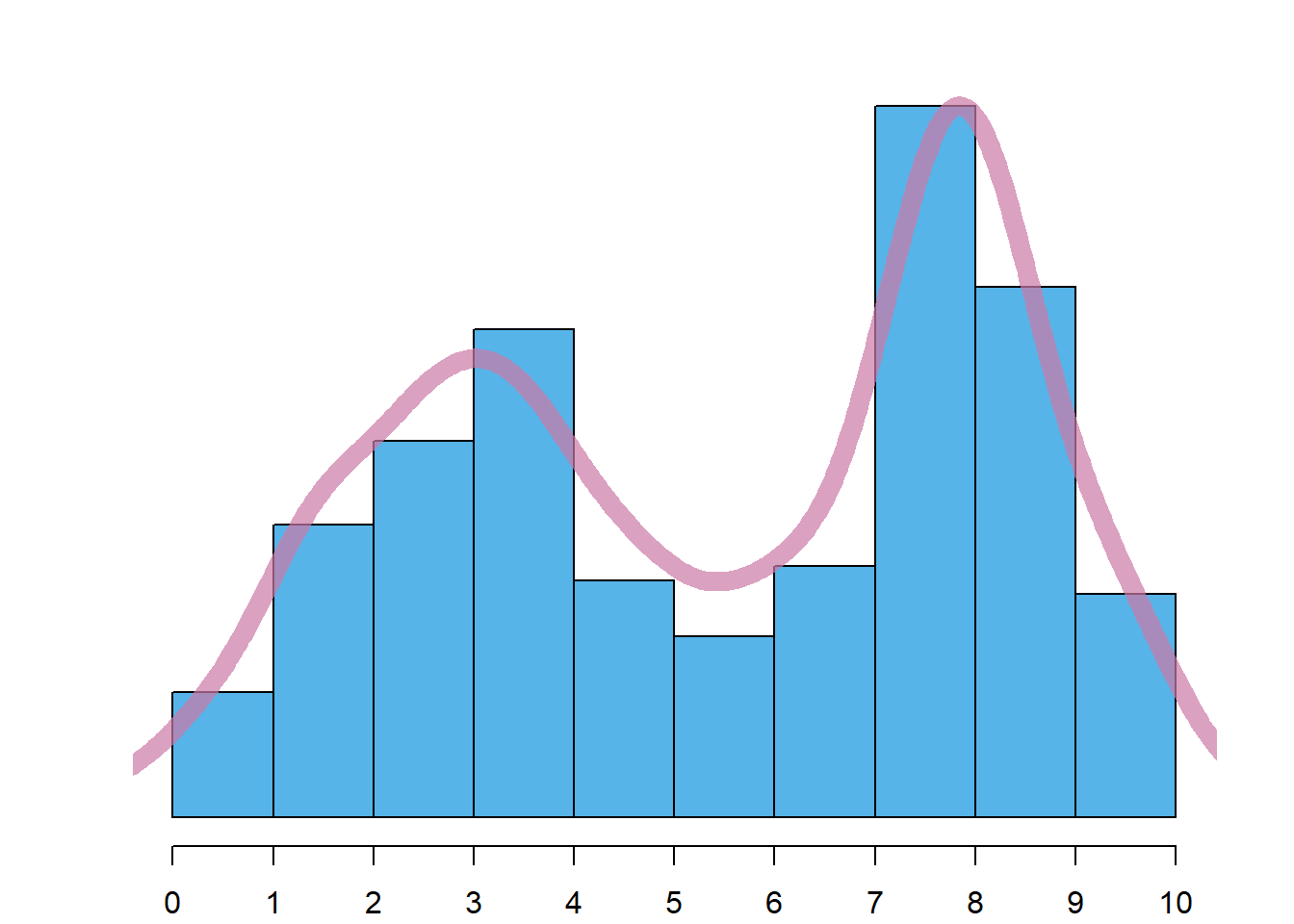
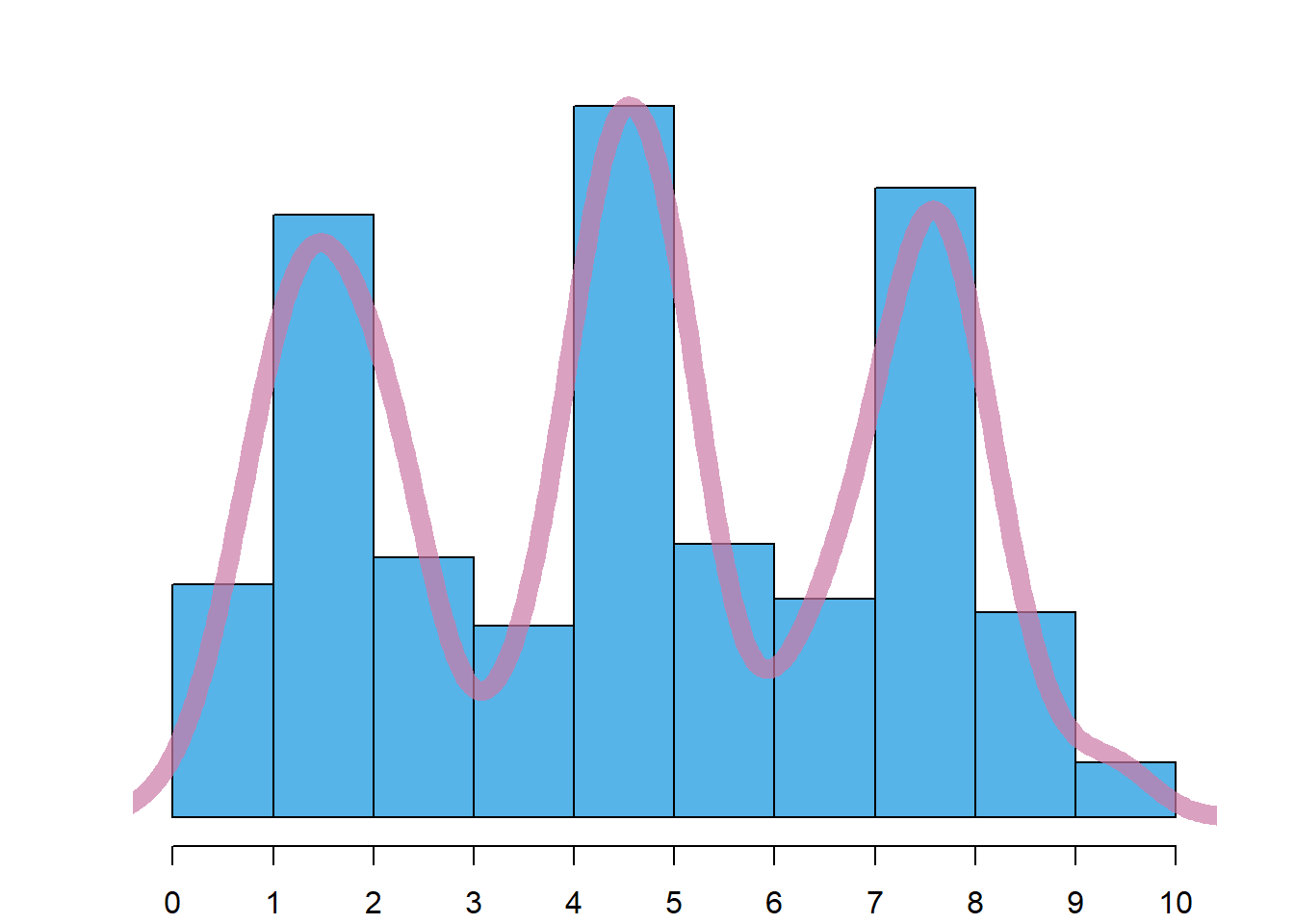
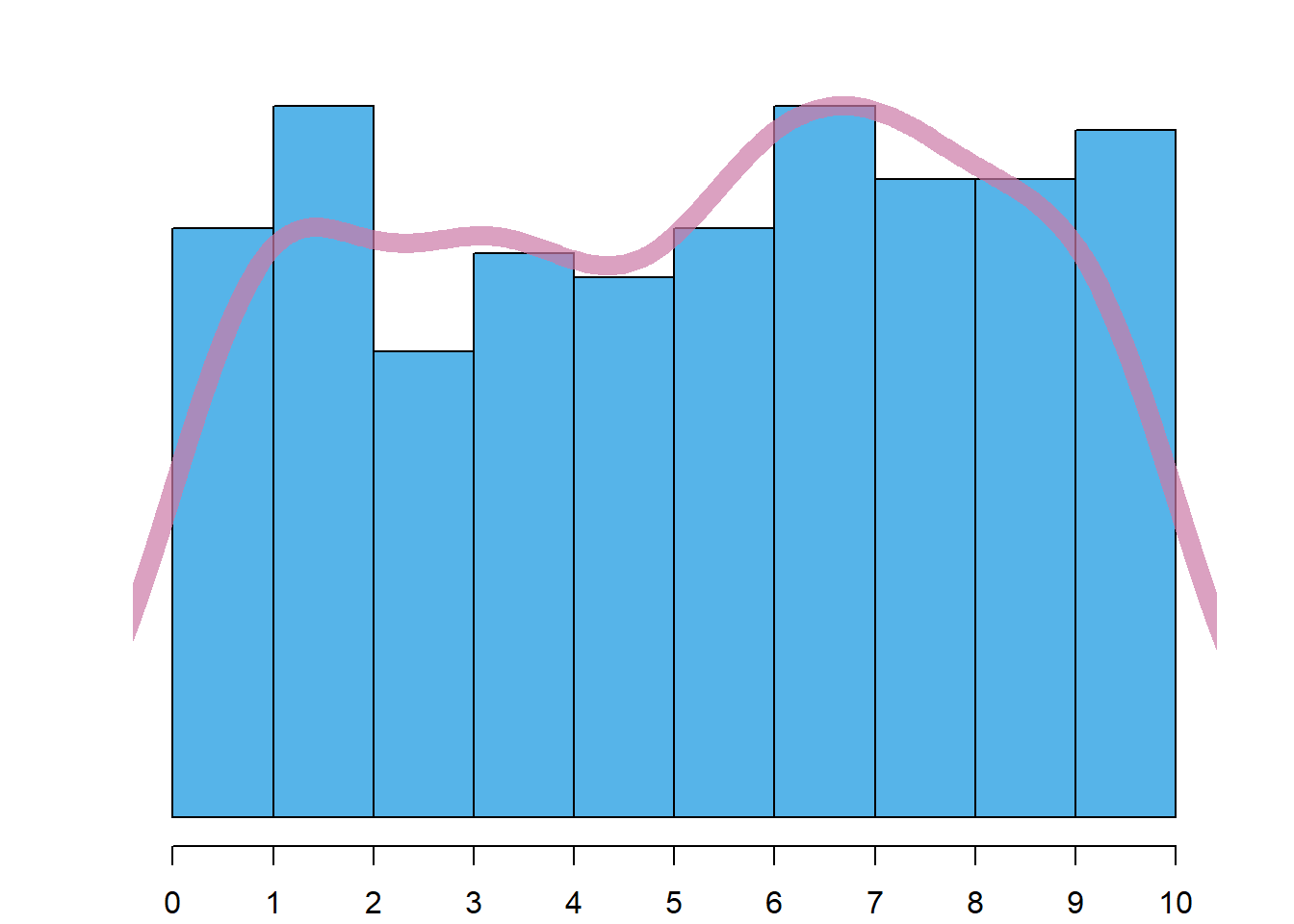
Para ajudar a visualizar o tipo de moda, deve imaginar-se uma curva suave sobre o histograma, tal como as apresentadas na Figura 4.4. Uma boa forma de uma fazer é imaginar uma corda flexível repousada sobre as barras.
Simetria
Um outro aspeto que o histograma permite avaliar é a simetria da distribuição dos dados em torno dos valores centrais. Neste caso, há 3 situações:
Distribuição assimétrica à esquerda: o histograma apresenta uma cauda esquerda mais prolongada, tal como na Figura 4.5 (a).
Distribuição assimétrica à direita: naturalmente é o oposto da anterior, apresentando o histograma uma cauda direita mais prolongada, tal como na Figura 4.5 (b).
Distribuição simétrica: neste caso, os dados distribuem-se de forma aproximadamente simétrica em torno dos valores centrais, tal como é o caso da Figura 4.5 (c). Note-se que existem quase sempre pequenas assimetrias.
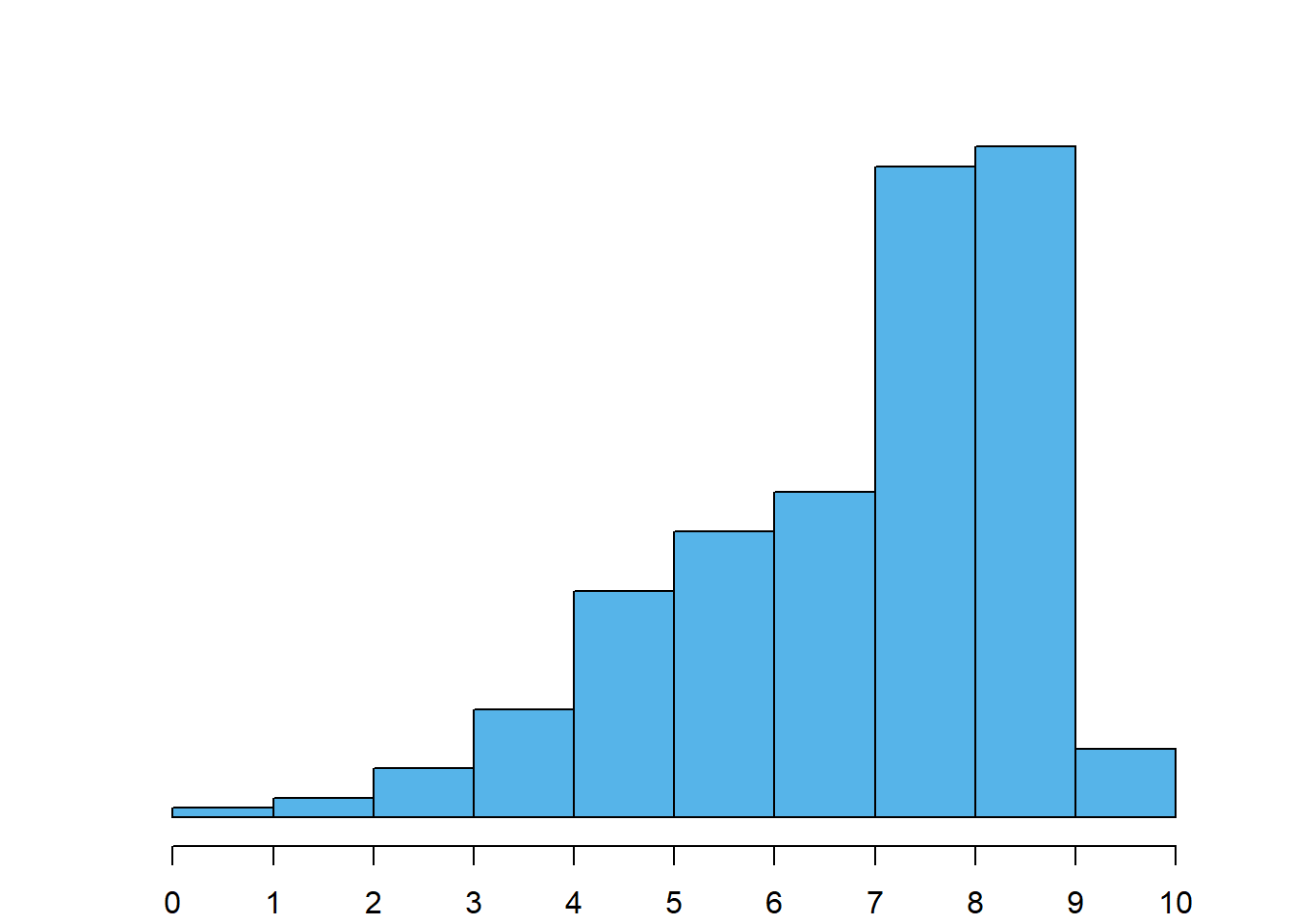
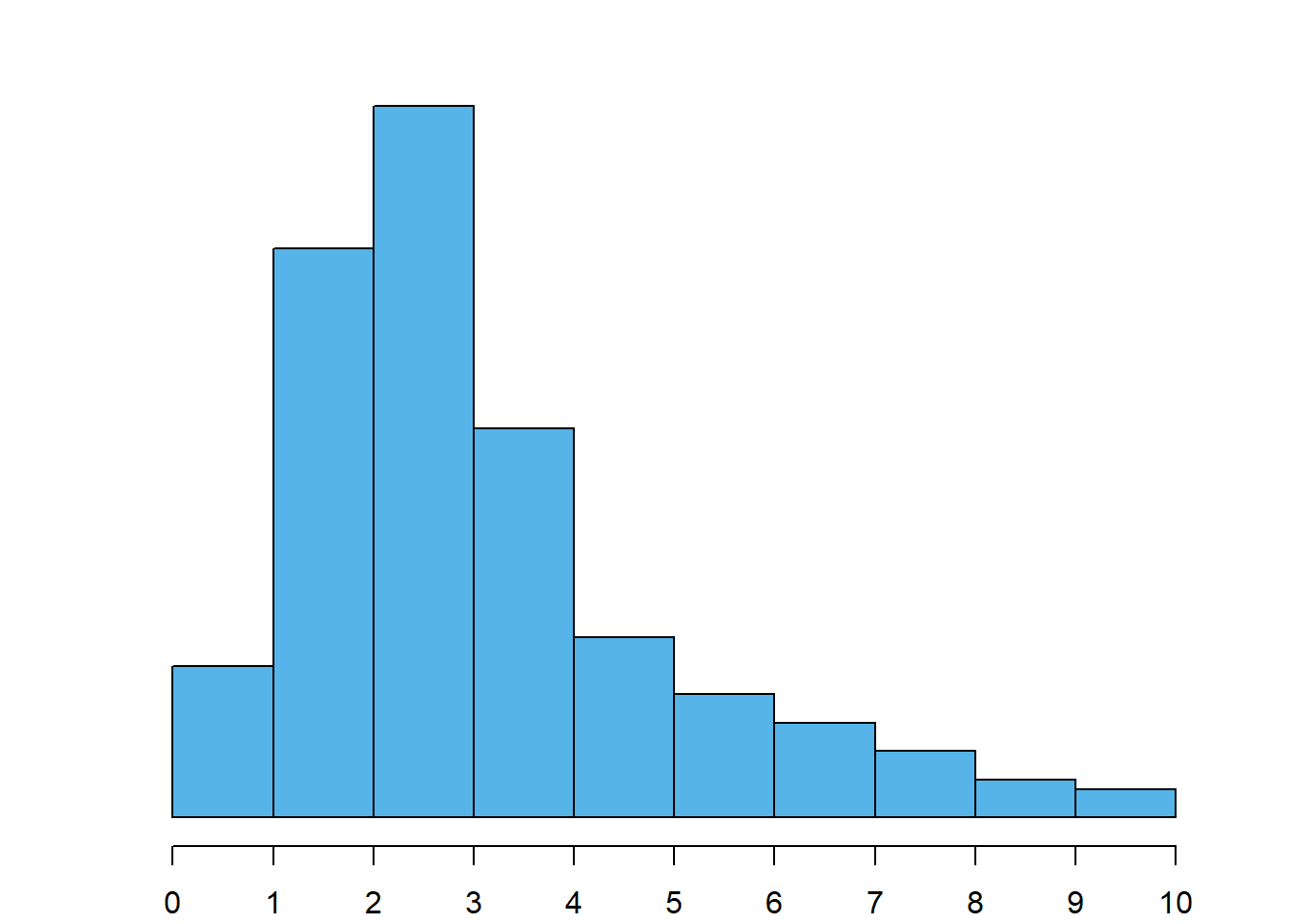
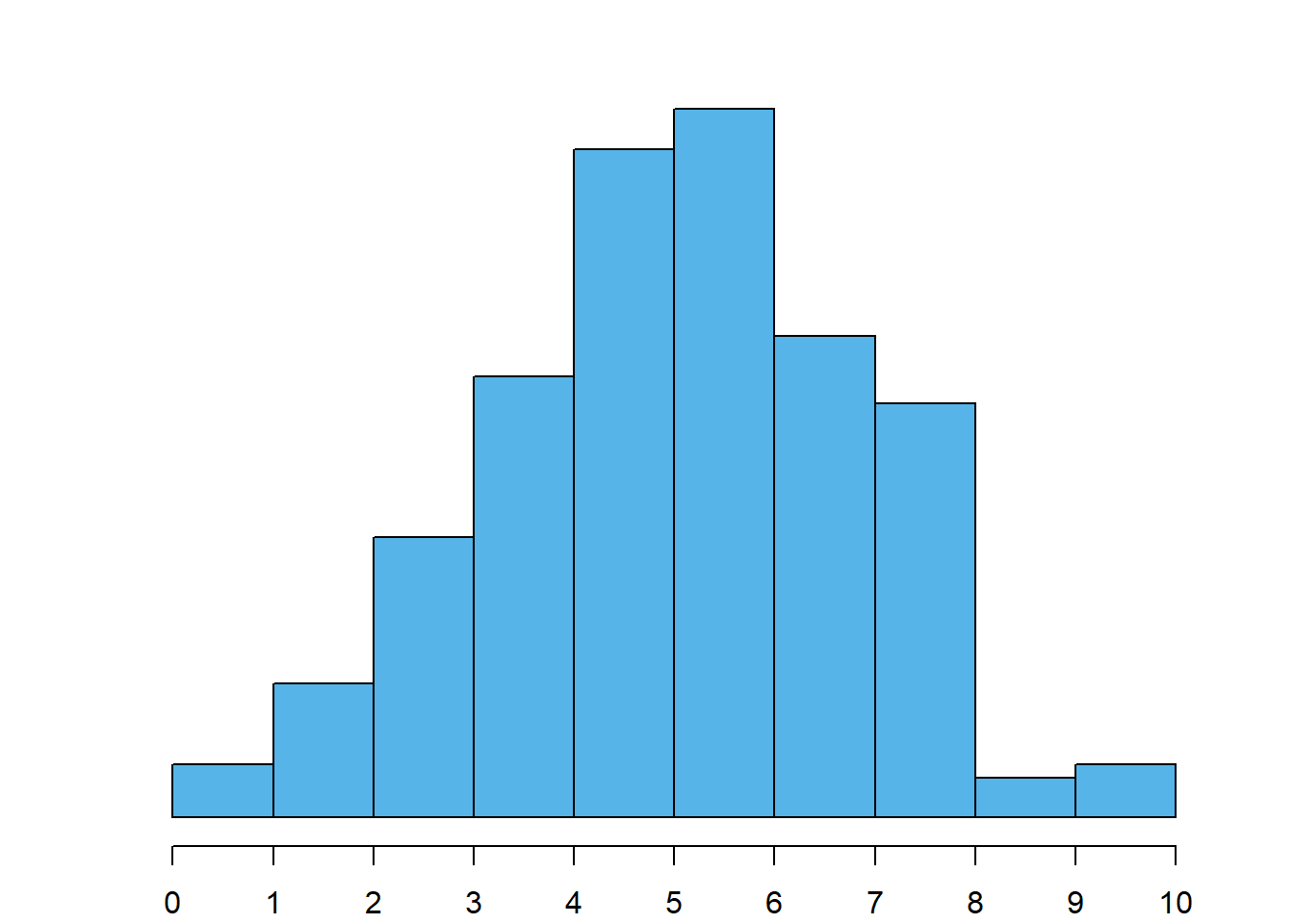
A assimetria diz-se à esquerda ou à direita conforme a cauda mais prolongada esteja desse mesmo lado. Não tem nada que enganar!
Observações incomuns
Outra característica que pode ser identificada no histograma é a presença de observações incomuns, vulgarmente designadas no termo inglês outliers.
Um observação (ou conjunto de observações) é incomum quando se diferenciam de forma bastante evidente das restantes. Na Figura 4.6 mostram-se um exemplo da situação, sendo evidente a presença de algumas observações na cauda direita, claramente destacadas do conjunto principal.
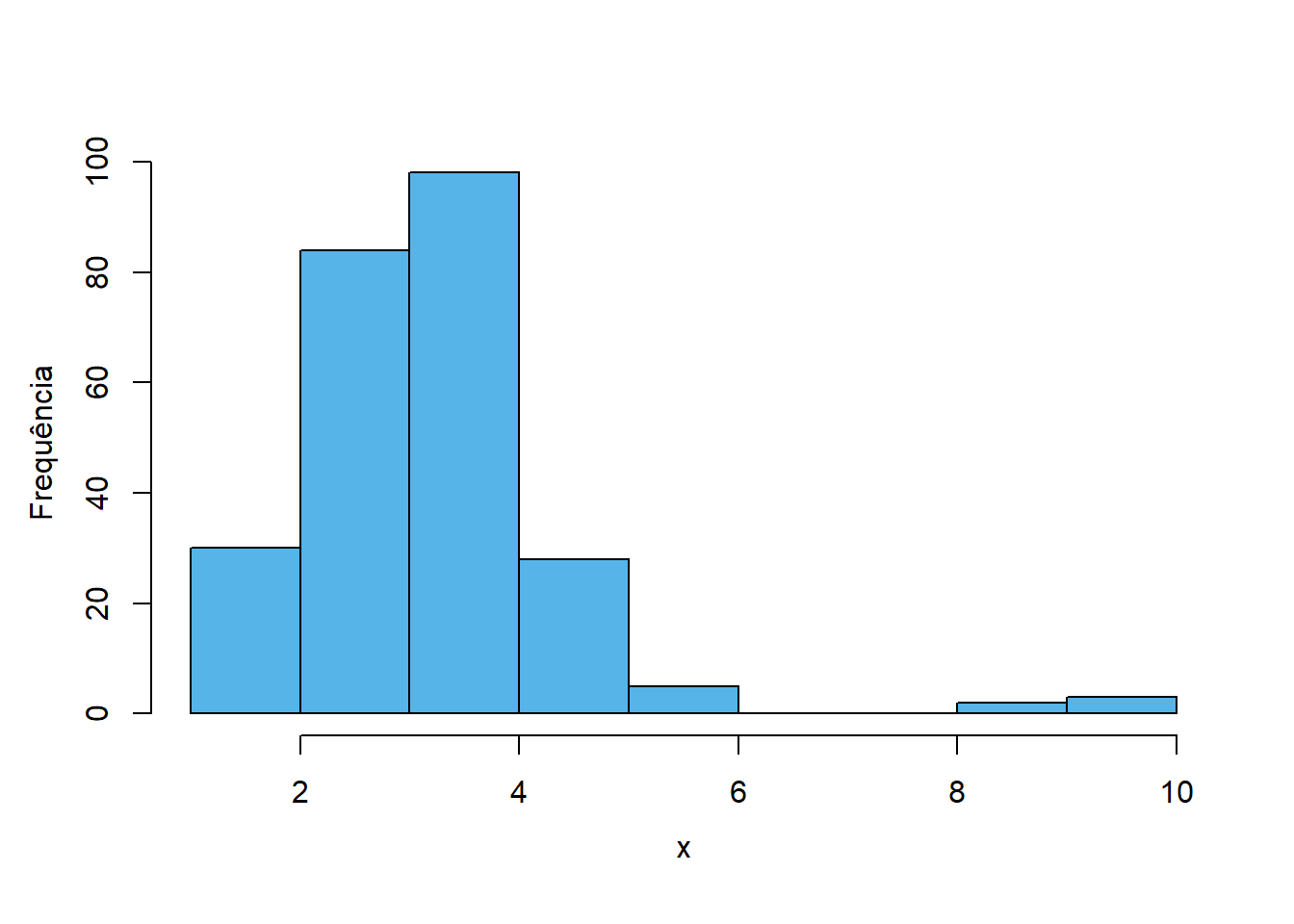
A identificação de observações fora do comum é importante por variadas razões:
Deteção de erros: uma das origens das observações incomuns são erros de medição ou de registo dos dados, sobretudo quando envolve processos manuais. A identificação destas observações é uma oportunidade para confirmar ou não que os valores estão corretos.
Deteção de assimetrias extremas: caso se confirme que não há erros, os valores incomuns podem indicar assimetrias extremas nos dados e levar à escolha de métodos adequados para lidar com elas, melhorando a qualidade da análise estatística.
Deteção de características interessantes: os valores incomuns podem revelar características desconhecidas da população que poderá ser interessante estudar.
O humorista Nuno Markl tem um programa de rádio e podcast intitulado O Homem que Mordeu o Cão, onde relata histórias bizarras que vão ocorrendo pelo mundo. De facto, quando o cão morde o homem é banal. A história é muito mais incomum e interessante quando acontece o contrário.
4.3 Localização e dispersão
Nas secções anteriores mencionaram-se os conceitos de centro, cauda, intervalo, etc., de maneira mais ou menos informal. Nesta secção serão formalizados esses conceitos com definições mais precisas.
Ao descrever um conjunto de dados é comum apresentar estatísticas de localização (por exemplo, a média) e estatísticas de dispersão (por exemplo, a amplitude dos dados). De facto, trata-se de dois parâmetros de grande importância na compreensão das distribuições dos dados.
4.3.1 Localização
Quando se apresentam estatísticas de localização, o termo refere-se ao valor à volta do qual os dados se distribuem, ou seja, onde estão localizados. Há várias formas de expressar a localização sendo as mais comuns a média, a mediana e a moda (já abordada na Secção 4.2.2).
Média
A média de um conjunto de dados desagrupados, normalmente denotada por \(\bar{x}\), pode ser calculada através da expressão:
\[\bar{x} = \frac{\sum_i x_i}{n} \tag{4.1}\]
É necessário distinguir a média populacional, denotado por \(\mu\), da média amostral, denotada por \(\bar{x}\):
A média populacional, \(\mu\), é uma constante definida para a população, normalmente desconhecida. Apenas pode ser calculada se se conhecer a população.
A média amostral, \(\bar{x}\), é calculada a partir de uma amostra, e pode ser tomada como uma estimativa da média populacional. Quando se descrevem dados, o termo média, quase sempre, se refere à média amostral.
Daquela definição resulta que a média é um valor localizado no centro dos dados que tem algumas propriedades interessantes:
A soma de todas as diferenças para a média é sempre 0, ou seja, \(\sum_i (x_i-\bar{x}) = 0\).
A soma do quadrado de todas as diferenças para uma constante \(c\), \(\sum_i (x_i-c)^2\), é mínima quando \(c = \bar{x}\).
Esta propriedades fazem da média o “centro de gravidade” de um conjunto de dados, sendo a medida de localização mais utilizada para descrever dados. Na Figura 4.7 pode visualizar-se a média do conjunto de dados utilizado anteriormente, juntamente com as observações da variável.
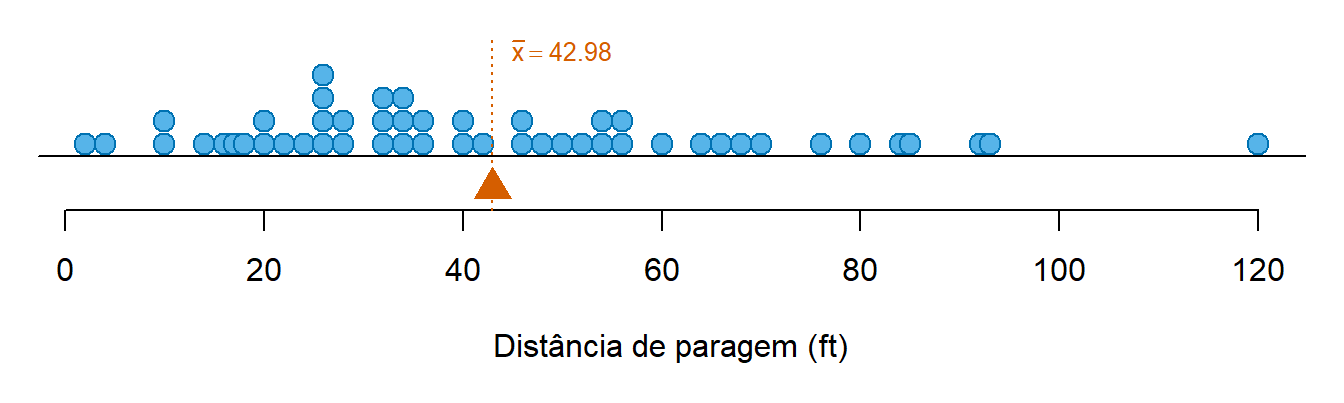
Devido à propriedades enunciadas acima, note-se como soma das distâncias dos pontos à média é igual à esquerda e à direita, sendo mais pequenas e em maior número à esquerda e maiores mas em menor número à direita, pois a distribuição é ligeiramente assimétrica à direita.
Utilizando os dados da distância de paragem apresentados na Secção 4.1.1 o cálculo da média é feito da seguinte forma:
\[\bar{x} = \frac{2+10+4+22+\cdots+85}{50} = 42.98\]
Uma outra situação que ocorre com alguma frequência é ter uma situação de dados discretos agrupados, como no exemplo Secção 4.1.3. Neste caso, o cálculo da média pode ser feito a partir da tabela de frequências (Tabela 4.2) através da expressão
\[\bar{x}=\frac{\sum_k{x_k f_k}}{n}=\sum_k{x_k f'_k} \tag{4.2}\]
\[\bar{x} = \frac{17\times1+18\times1+19\times8+\cdots+23\times4}{50} = 20.343\] Multiplicar as idades pelo número de ocorrências é equivalente a somar uma idade o número de vezes que ela ocorre, pelo que a Equação 4.2, para dados discretos agrupados, é equivalente à expressão Equação 4.1 para dados desagrupados.
No caso de dados contínuos agrupados, como foi visto, o agrupamento implica perda de informação, logo, não é possível calcular a média de forma equivalente à situação de dados desagrupados. Uma forma de estimar um valor aproximado para a média é utilizar a Equação 4.2 substituindo \(x_k\) pelos pontos centrais de cada classe. No caso da Tabela 4.1, ficaria:
\[\bar{x} = \frac{10\times10+30\times18+50\times11+\cdots+110\times1}{50} = 41.6\]
Como pode verificar, o valor difere ligeiramente do calculado anteriormente pela expressão Equação 4.1, que foi 42.98. Daí ser sempre preferível ter os dados desagrupados e efetuar os cálculos a partir destes.
Mediana
Uma outra medida de localização comum é a mediana. A mediana tem uma definição muito simples, sendo o valor central, depois dos dados ordenados (ou, no caso de um número par de observações, a média dos dois valores centrais).
Para calcular a mediana, o procedimento é então:
- Ordenar os dados
- Determinar o valor central (número ímpar de observações) ou a média dos dois valores centrais (número par de observações).
Considere-se a seguinte amostra: 54, 51, 50, 47, 57, 49, 53 (número ímpar de observações)
Num primeiro passo, devem ordenar-se as observações: 47, 49, 50, 51 , 53, 54, 57
A mediana é o valor central, ou seja, 51.
Considere-se agora a seguinte amostra: 50, 50, 48, 41, 57, 51, 55, 58 (número par de observações)
Num primeiro passo devem, ordenar-se as observações: 41, 48, 50, 50 , 51 , 55, 57, 58
A mediana é a média dos dois valores centrais, ou seja, \(\frac{50 + 51}{2} =\) 50.5.
Quantis
A mediana é um caso particular de um quantil, sendo o quantil \(Q_p\) definido como o ponto da distribuição abaixo do qual se situa uma proporção de observações igual a \(p\).
Logo, a mediana é o quantil \(Q_{\frac{1}{2}}\).
De facto, é comum o valor de \(p\) ser definido como uma fração, \(p=\frac{k}{q}\). Dependendo do valor de \(q\), os quantis têm nomes mais específicos:
- Quartis para \(q=4\): dividem os dados em quatro partes com, aproximadamente, o mesmo número de observações.
- Decis para \(q=10\): dividem os dados em 10 partes.
- Percentis para \(q=100\): dividem os dados em 100 partes.
No caso dos quartis, teremos os quartis \(Q_0\) (mínimo), \(Q_1\) (1.º quartil), \(Q_2\) (2.º quartil ou mediana), \(Q_3\) (3.º quartil) e \(Q_4\) (máximo). Estas estatísticas irão ser utilizadas mais à frente.
Para não haver confusão entre quantil e quartil, ambos notados com \(Q\), adota-se o seguinte critério:
se \(Q\) for seguido de uma fração ou proporção, é um quantil, por exemplo, \(Q\frac{1}{20}\) ou \(Q_{0.95}\).
Caso seja seguido de um inteiro entre 0 e 4 será um quartil, por exemplo, \(Q_3\).
Para calcular o quantil \(Q_p\) utiliza-se a seguinte expressão:
\[ Q_p = x_{\lfloor h \rfloor} + ( h - \lfloor h \rfloor)( x_{\lceil h \rceil} - x_{\lfloor h \rfloor}) \tag{4.3}\]
com
\[h = (n-1) p + 1 \tag{4.4}\]
Considere-se novamente a amostra: 54, 51, 50, 47, 57, 49, 53
Começamos por ordenar as observações: 47, 49, 50, 51, 53, 54, 57
Calcule-se agora o 3.º quartil, ou seja, \(p=0.75\).
Através da Equação 4.4, calcule-se, \(h = (7 - 1) * 0.75 + 1 = 5.5\), \(\lfloor h \rfloor = 5\) e \(\lceil h \rceil = 6\), sendo \(x_{\lfloor h \rfloor}=x_{5} = 53\) e \(x_{\lceil h \rceil}=x_{6} = 54\).
Podemos agora calcular \(Q_3\) utilizando a Equação 4.3:
\[Q_3 = 53 + (5.5 - 5) * (54 - 53) = 53.5\]
4.3.2 Dispersão
A dispersão de um conjunto de dados refere-se à variabilidade. Dados com pouca variabilidade estão concentrados num intervalo pequeno e dados com muita variabilidade dispersam-se por um grande intervalo. Naturalmente, os termos grande e pequeno são relativos e devem ser interpretadas no contexto dos dados.
Vão-se analisar algumas medidas de dispersão: a amplitude amostral, a amplitude interquartis, o desvio padrão e a variância.
Amplitude
A amplitude amostral é simplesmente a diferença entre a observação máxima e a observação mínima.
\[A = x_{max}-x_{min} \tag{4.5}\]
Se a amplitude é pequena, os dados estão concentrados tendo pouca dispersão e, se a amplitude for grande, estão mais dispersos.
Por exemplo no caso das distâncias de paragem da Secção 4.1.1 o valor mínimo é \(x_{min}=2\) e o máximo é \(x_{max}=120\). Logo, \(A = x_{max}-x_{min} = 120-2 = 118\).
A amplitude é uma medida que é muito afetada por valores atípicos nos extremos. No exemplo acima, caso a observação máxima (120) fosse eliminada, o máximo desta amostra seria 93, reduzindo a amplitude consideravelmente.
Amplitude interquartis
A amplitude interquartis é definida como a diferença entre o terceiro e o primeiro quartis.
\[AIQ=Q_3-Q_1 \tag{4.6}\]
Por esse motivo, já não é tão afetada por valores extremos. No exemplo que tem vindo a ser seguido (distâncias de paragem) o primeiro quartil é \(Q_1 = 26\), o terceiro quartil é \(Q_3 = 56\) resultado numa amplitude interquartis \(AIQ = 30\).
Diagrama de extremos e quartis
O diagrama de extremos e quartis, vulgarmente designado em inglês por box plot, serve para representar algumas das estatísticas já apresentadas (mínimo, máximo, quartis, mediana). É um diagrama bastante útil e que fornece um resumo visual dos dados.
Na Figura 4.8 apresenta-se o diagrama de extremos e quartis para as distâncias de paragem e a figura Figura 4.9 mostra o significado dos vários componentes do diagrama. Os diagramas foram colocados na horizontal por uma questão prática, mas podem ser representados na vertical, transpondo os eixos.
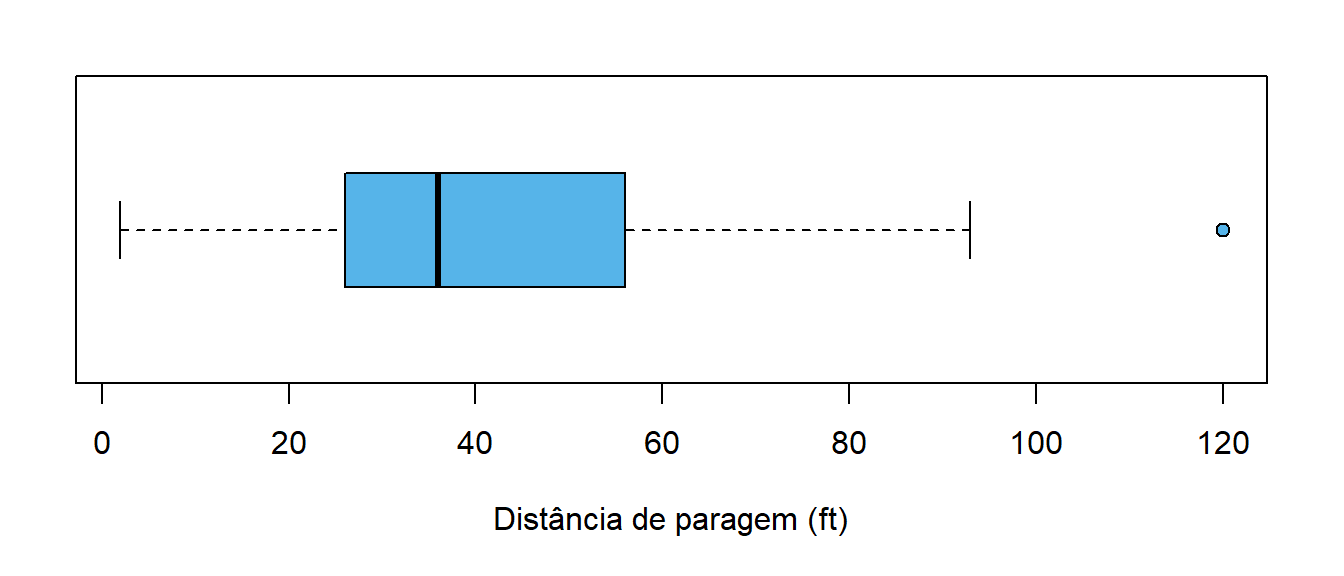
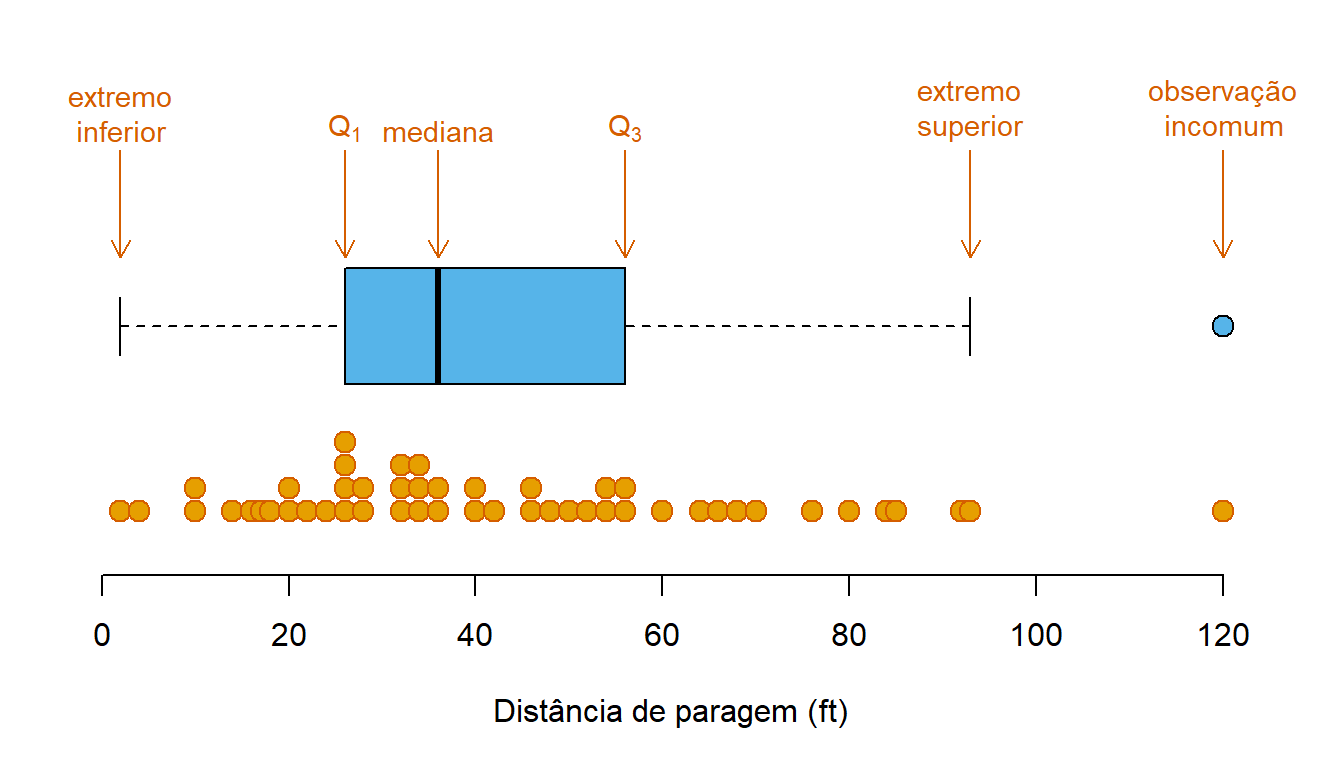
No diagrama, a caixa representa a amplitude interquartis e contém, aproximadamente, 50% das observações da amostra, estando as 25% mais pequenas à esquerda da caixa e as 25% maiores à direita da caixa.
A partir do diagrama obtém-se uma ideia precisa do centro, da variabilidade, de eventuais observações incomuns e da assimetria da distribuição, sendo uma boa representação para comparar vários grupos de observações.
Por regra, os extremos do diagrama podem ir até à observação mais extrema que não ultrapasse \(r\) vezes a amplitude interquartis. Na implementação do R, por omissão, é utilizado \(r = 1.5\). Neste caso, sendo \(Q_1 = 26\), \(Q_3 = 56\) e \(AIQ = 30\) os extremos poder-se-iam estender até \(26 - 1.5 \times 30 = -19\), à esquerda, e até \(56 + 1.5 \times 30 = 101\), à direita. Todas as observações inferiores a -19 ou superiores a 101 seriam representadas com pontos, fora dos extremos (observações incomuns).
Variância e desvio padrão
As últimas medidas de dispersão que se apresentam são a variância e desvio padrão.
Referiu-se a propósito da média que quando se fazia \(c = \bar{x}\) a soma \(\sum_i (x_i-c)^2\) era mínima. De facto, nessa situação, aquela soma é conhecida por soma dos desvios quadráticos ou SDQ.
\[SDQ = \sum_i (x_i-\bar{x})^2 \tag{4.7}\]
Dividindo aquela soma pelo número de observações menos 1 obtém-se uma medida de dispersão denominada variância amostral e notada por \(s^2\).
\[s^2 = \frac{\sum_i (x_i-\bar{x})^2}{n-1} \tag{4.8}\]
Esta estatística é uma forma de medir a dispersão, pois quanto mais dispersas estiverem as observações, mais afastadas estarão da média, implicando valores elevados de variância.
Tal como no caso da média, existe a variância amostral, \(s^2\) e a variância populacional, notada com \(\sigma^2\). A relação entre as duas é exatamente a mesma referida para a média: por norma, a variância populacional é uma constante desconhecida que pode ser estimada através da variância amostral. Caso se esteja perante uma população, a expressão é ligeiramente diferente, sendo
\[\sigma^2 = \frac{\sum_i (x_i-\mu)^2}{n} \tag{4.9}\]
Alternativamente, trabalhando a Equação 4.8, a variância pode ser calculada através da seguinte expressão equivalente:
\[s^2 = \frac{\sum_i x_i^2-n\bar{x}^2}{n-1} \tag{4.10}\]
Por norma, a expressão Equação 4.10 é mais prática para efetuar cálculos manuais.
A variância nunca é negativa. No mínimo, se todas as observações forem iguais, ou seja, se não houver dispersão, a variância é zero.
As unidades de medida da variância são as unidades de medida da variável ao quadrado. Por exemplo, se a variável em causa for a idade, em anos, a variância é expressa em anos2.
Esta última propriedade torna os valores da variância pouco intuitivos, devido à estranheza das dimensões. Por esse motivo, em alternativa à variância podemos expressar a dispersão em termos do desvio padrão que, simplesmente, é definido como a raiz quadrada da variância e é expresso nas mesmas unidades da variável.
\[s = \sqrt{s^2} \tag{4.11}\]
Considere-se novamente amostra: 50, 50, 48, 41, 57, 51, 55, 58
Para calcular a variância é necessário calcular previamente a média, \(\bar{x}= 51.25\).
Podemos também calcular
\[\sum_i x_i^2 = 50^2+50^2+48^2+41^2+57^2+51^2+55^2+58^2 = 21224\] Agora estamos em condições de calcular a variância e o desvio padrão:
\[s^2 = \frac{21224 - 8 \times 51.25^2}{7} \approx 30.214\]
\[s = \sqrt{30.214} \approx 5.497\]
Uma outra vantagem do desvio padrão está numa propriedade derivada da desigualdade de Chebyshev: se definirmos um intervalo à volta da média com uma meia amplitude 3 desvios padrão, temos a garantia de encontrar a quase totalidade das observações dentro desse intervalo1.
Na Figura 4.10 pode visualizar-se esta propriedade para o exemplo das distâncias de paragem que se tem vindo a tratar.
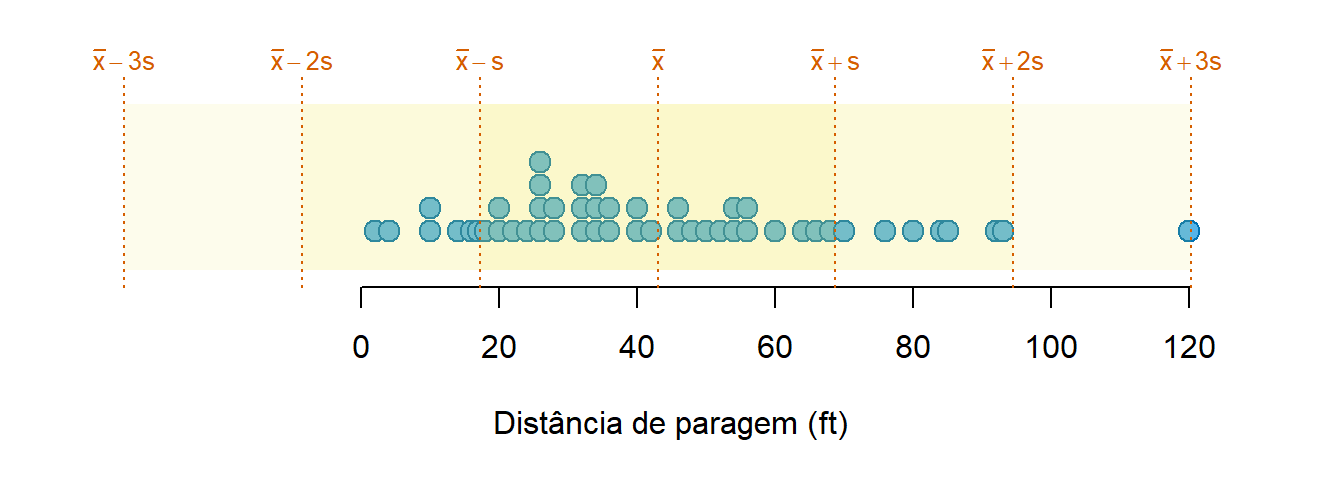
Neste caso, a totalidade das observações está dentro do intervalo de 3 desvios padrão em torno da média (nem sempre acontece, mas, geralmente, a quase totalidade vai estar). Note-se que, mesmo reduzindo o intervalo para 2 desvios padrão em torno da média, apenas 1 observação está fora do intervalo.
Na prática, esta propriedade permite inferir que, para qualquer variável, observações afastadas da média mais de 2 desvios padrão, são raras e, afastadas mais de 3 desvios padrão, são muito raras. Dever-se-á ter esta constatação sempre presente durante a análise estatística.
4.3.3 Observações incomuns e valor Z
Decorre das propriedades do desvio padrão referidas no final da Secção 4.3.2 que a distância entre uma observação e a média, no contexto do valor do desvio padrão permite avaliar quão incomum é a observação.
Uma forma eficiente de avaliar a distância de uma observação à média é através do cálculo do seu valor Z, uma operação designada por padronização ou normalização (embora a normalização possa significar outros conceitos). O valor Z de uma observação, \(x\) pode ser calculado com
\[z = \frac{x-\bar{x}}{s}\]
O valor Z é adimensional e indica de forma expedita quantos desvios padrão a observação está acima da média (\(z\) positivo) ou abaixo da média (\(z\) negativo). Embora, quer o histograma, quer o diagrama de extremos e quartis permitam detetar observações incomuns, os valores Z são mais uma ferramenta ao dispor do analista.
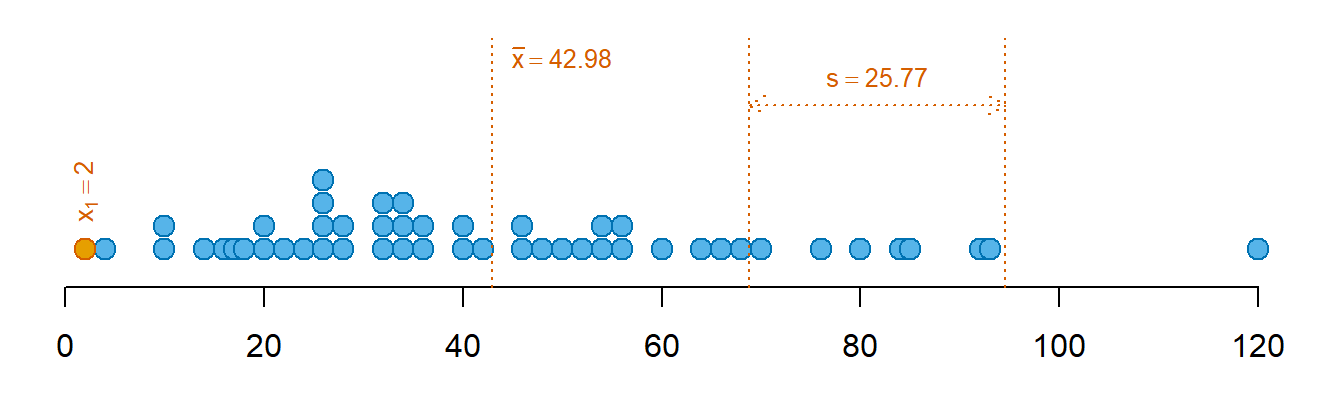
Considere-se a primeira observação das distâncias de paragem, \(x_1 = 2\). Relembre-se que \(\bar{x} = 42.98\) e \(s = 25.77\). O valor z será:
\[z_1 = \frac{2 - 42.98}{25.77} = -1.59\]
Esta valor significa que a observação está -1.59 desvios padrão abaixo da média (Figura 4.11).
Note-se que a padronização não altera a distância relativa entre as observações. Se a padronização for aplicada a toda a distribuição, os dados padronizados terão média igual a 0 e desvio padrão igual a 1. Tal pode ser facilmente demonstrado introduzindo a transformação nas equações 4.1 e 4.8. A Figura 4.11 ilustra este ponto, utilizando o exemplo das distâncias de paragem.
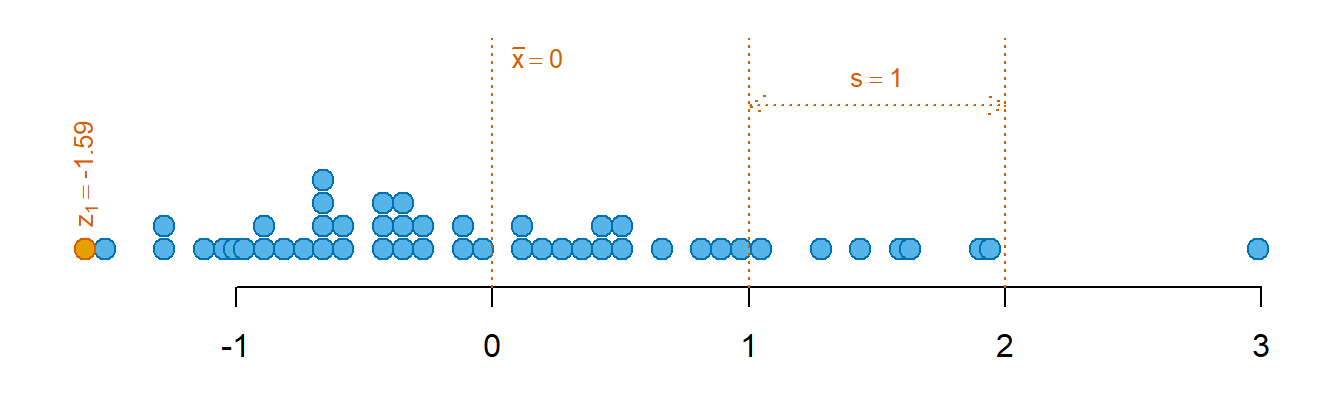
Regra geral, uma observação cujo valor Z, em termos absolutos, seja superior a 3, ou seja, \(|z| > 3\), é incomum. Tais observações são raras e podem indicar erros nos dados ou características interessantes da distribuição, tal como referido na Secção 4.2.2.
Da mesma forma, valores Z absolutos entre 2 e 3, são também algo incomuns e devem merecer um segundo olhar do analista.
4.4 Estatísticas robustas
As estatísticas calculadas a partir dos dados devem possuir algumas propriedades que as torne adequadas à análise que se pretende efetuar. Uma dessas propriedades é a robustez. A robustez consiste na propriedade do valor da estatística não ser muito afetado por observações incomuns.
Dos estimadores descritos nas secções anteriores, a mediana e a amplitude interquartis são estatísticas robustas. Já a média e o desvio padrão (ou variância) não são estatísticas robustas.
Classificação quanto à robustez:
- Robustas: mediana, amplitude interquartis.
- Não robustas: média, desvio padrão (ou variância).
Considere-se novamente o conjunto de dados relativo às distâncias de paragem. Para se ilustrar a questão da robustez, vão calcular-se as quatro estatísticas mencionadas, em 4 cenários diferentes:
- Dados originais.
- Dados originais mais 1 observação igual a 172 (aproximadamente, o máximo dos dados originais mais 2 desvios padrão)
- Dados originais mais 1 observação igual a 223 (máximo mais 4 desvios padrão)
- Dados originais mais 1 observação igual a 275 (máximo mais 6 desvios padrão)
A Tabela 4.3 mostra o resultado dos cálculos para os cenários enumerados.
| Média | Desvio padrão | Mediana | AIQ | |
|---|---|---|---|---|
| Cenário 1 (dados originais) | 42.98 | 25.77 | 36 | 30 |
| Cenário 2 (dados e 172) | 45.51 | 31.26 | 36 | 32 |
| Cenário 3 (dados e 223) | 46.51 | 35.86 | 36 | 32 |
| Cenário 4 (dados e 275) | 47.53 | 41.31 | 36 | 32 |
Como pode verificar, as estatísticas robustas (mediana e AIQ), ou não se alteram, ou apenas se alteram ligeiramente. Já as estatísticas não robustas são muito sensíveis a observações extremas, mesmo que, como é o caso, seja apenas 1 observação.
Isto não quer dizer que as estatísticas não robustas são de evitar, pois possuem outras propriedades desejáveis. A média e o desvio padrão são estatísticas importantes com inúmeras aplicações práticas. Simplesmente, não são robustas, o que as torna pouco adequadas quando a robustez for uma propriedade importante.
Tipicamente, se os dados puderem conter observações extremas, devem valorizar-se estatísticas robustas. Por exemplo, se quisermos avaliar o rendimento típico das famílias, a estatística mais adequada é a mediana, pois a média é afetada pelas observações extremas que ocorrem na cauda direita desta distribuição. Há sempre famílias com rendimentos atípicos muito elevados que vão fazer com que o valor da média tenha pouco significado.
Se tiver 10 pessoas em que 9 têm um rendimento igual a 10 e a última tem um rendimento igual a 100, a mediana é 10 e a média é 19. Claramente, a média não é representativa do rendimento típico.
Média, mediana e simetria
Uma consequência do que foi afirmado acima acerca da média e da mediana está expresso na Figura 4.12. A figura recupera os dados da Figura 4.5 e acrescenta a posição da média e da mediana. Acrescentou-se igualmente uma linha de densidade estimada (como o conceito de densidade ainda não foi apresentado, deve entendê-la como um sinónimo de concentração de observações numa vizinhança).
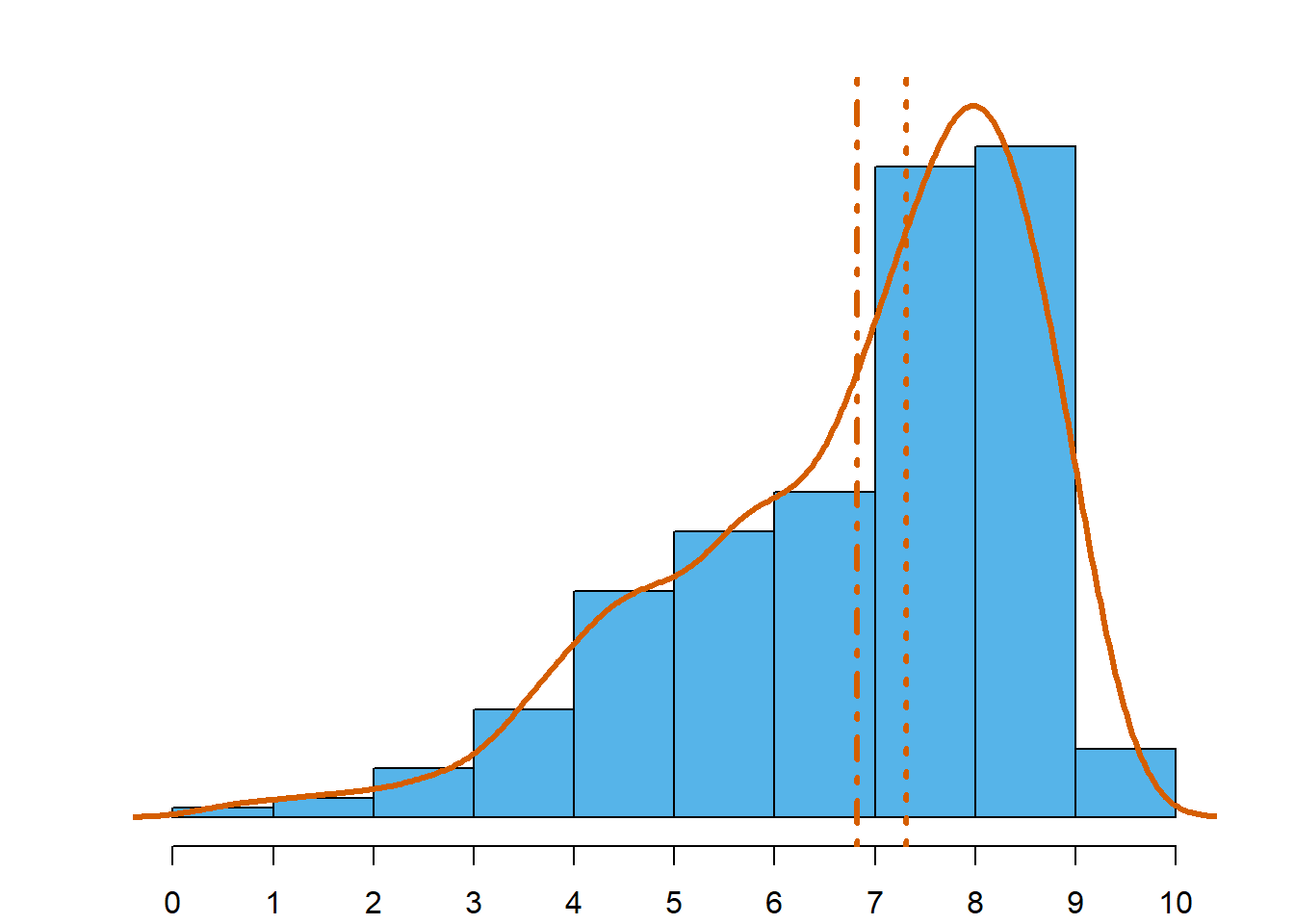
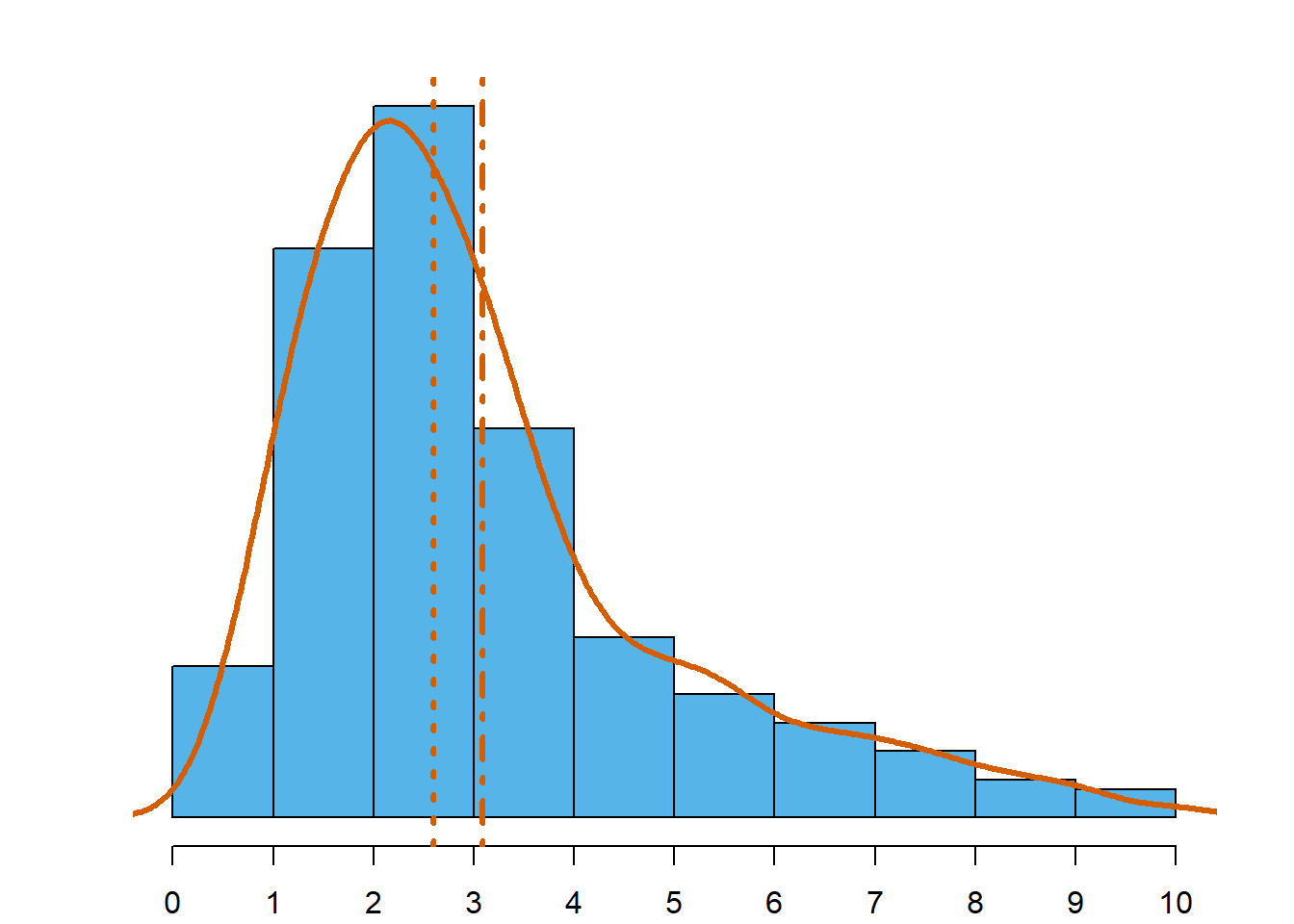
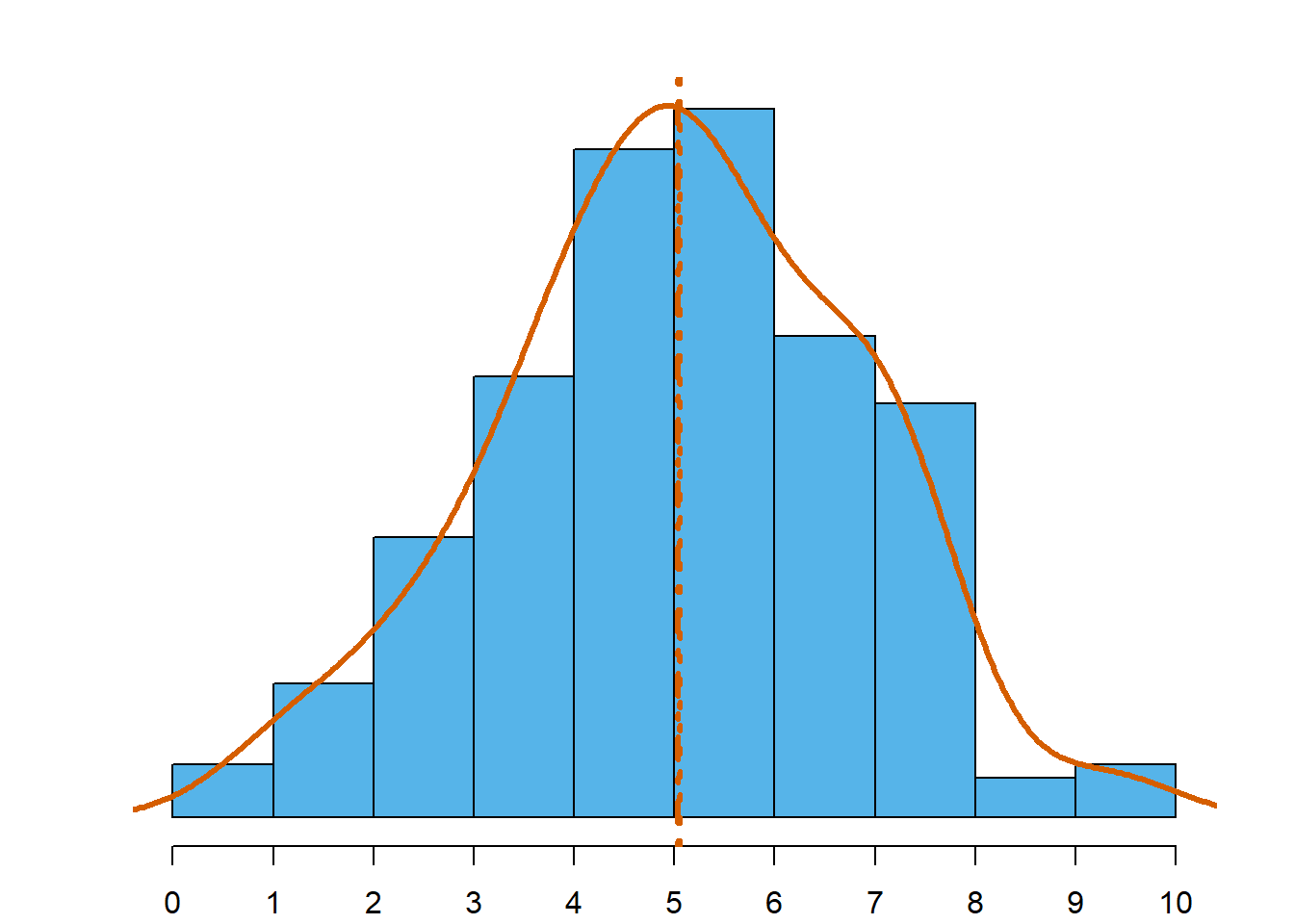
Os gráficos ilustram como se posicionam média e mediana, em termos relativos, quando a distribuição é assimétrica. Enquanto que numa distribuição aproximadamente simétrica, moda, mediana e média estão sensivelmente no mesmo ponto (Figura 4.12 (c)), numa distribuição assimétrica as 3 estatísticas tomam valores diferentes. Numa distribuição assimétrica à esquerda, a média é menor que a mediana, e esta é menor que a moda (Figura 4.12 (a)). Numa distribuição assimétrica à direita acontece o oposto: a média é maior que a mediana, que por sua vez é maior que a moda (Figura 4.12 (b)).
Com o aumento da assimetria, as estatísticas menos robustas deslizam em direção a uma das caudas, dependendo da assimetria.
Geralmente:
- Em distribuições aproximadamente simétricas: moda \(\approx\) mediana \(\approx\) média.
- Em distribuições assimétricas à esquerda: moda > mediana > média.
- Em distribuições assimétricas à direita: moda < mediana < média.
Tutoriais
Depois de ler este capítulo pode verificar como são implementados estes conceitos no ambiente computacional R. Os tutoriais listados abaixo estão diretamente relacionados com este capítulo.
| Tutorial | Descrição |
|---|---|
| Gráficos | Noções fundamentais sobre a elaboração de gráficos no R. |
| Histogramas | Construção e configuração de histogramas no R. |
| Diagramas de Extremos e Quartis | Construção e configuração de diagramas de extremos e quartis no R. |
Num intervalo centrado na média, com uma meia amplitude de 3 desvios padrão, é garantido encontrar \(8/9 \approx 88.9\%\) da distribuição dentro do intervalo. Na prática, está demonstrado que este limite é, em geral, muito conservador, havendo inúmeros casos em que a proporção de observações dentro do intervalo é muito próxima de 100%.↩︎