1 Metodologia e Dados
1.1 Introdução
A palavra estatística costuma estar associada a um de dois significados: num significado mais trivial, uma estatística refere-se a um facto numérico, por exemplo, quando se afirma que o rendimento mediano aumentou 2.1%.
O outro significado refere-se à disciplina científica, em que a Estatística é definida como um conjunto de métodos para recolher, analisar, apresentar e interpretar dados e, através deste processo, apoiar a tomada de decisão em ambientes que apresentem variabilidade.
Naturalmente, é neste último contexto que este texto se insere. Nesse contexto, a aplicação da Estatística segue uma metodologia que, em larga medida, se funde com o método científico:
Definição dos objetivos da análise, ou seja, o que se pretende investigar (frequentemente designados por questões ou hipóteses de investigação) e dos métodos a utilizar na análise.
Definição de um procedimento para a recolha dos dados necessários.
Recolha dos dados.
Análise dos dados.
Interpretação das análises e apresentação dos resultados.
Esta divisão é meramente conceptual pois as várias etapas nem são estanques nem puramente sequenciais. Por exemplo, o estabelecimento dos objetivos e a definição dos métodos de recolha dos dados têm que estar em estreita articulação. Frequentemente, surgem dificuldades não previstas na recolha dos dados que obrigam à redefinição do procedimento de recolha ou até mesmo à reformulação dos objetivos estabelecidos inicialmente. Quase sempre há também restrições económicas ou temporais com influência no planeamento dos trabalhos a desenvolver.
O resto deste capítulo aborda diferentes questões relacionadas com os pontos 1 a 3.
1.2 Tipos de dados
1.2.1 Escalas de medição
Sendo a Estatística uma ciência que lida com dados, é necessário conhecer os diversos tipos de dados e as suas características. A forma mais útil de o fazer é classificar os dados segundo a escala em que são expressos.
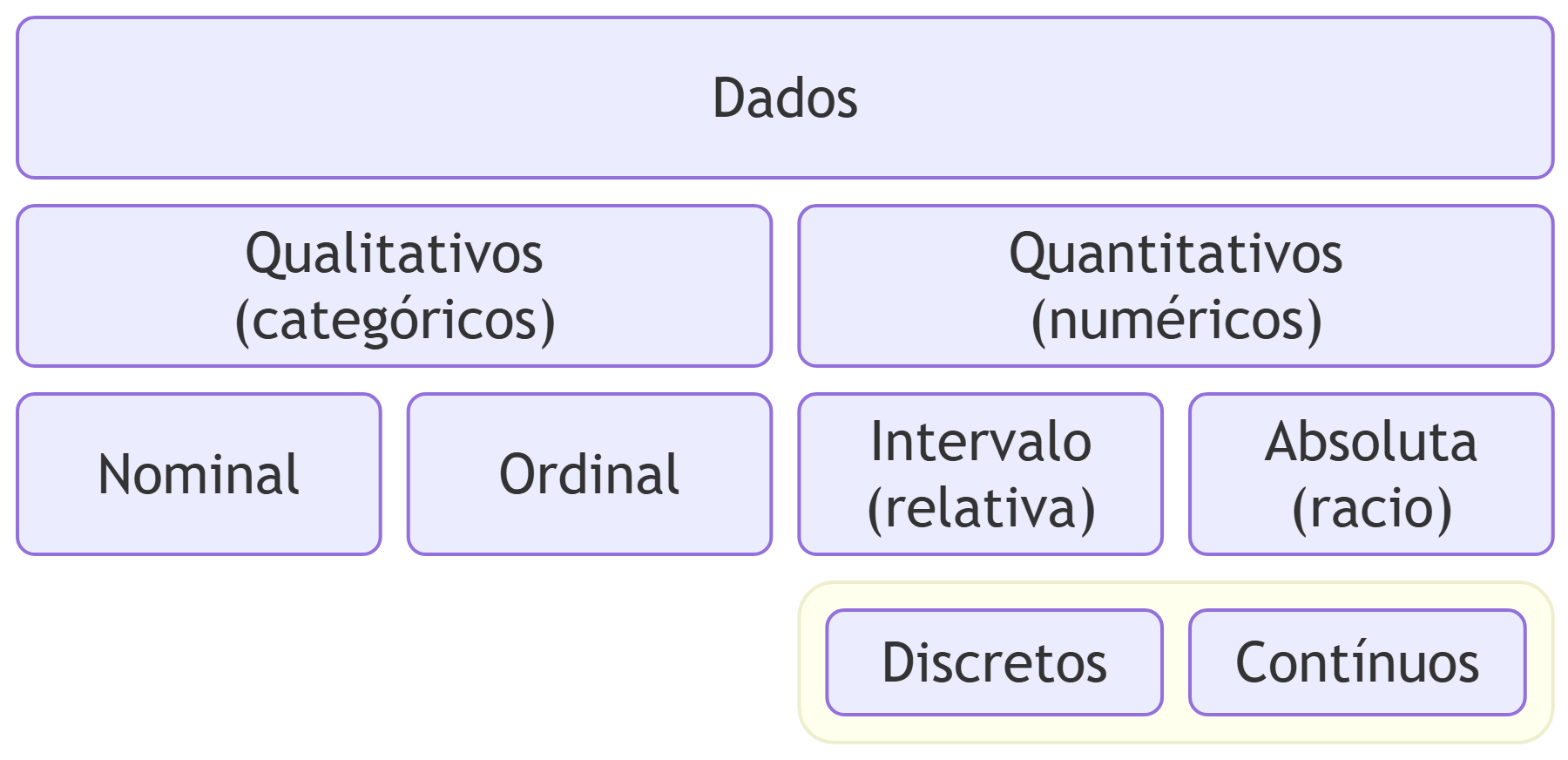
É comum identificar quatro escalas de medição agrupadas em duas categorias principais, tal como esquematizado na Figura 1.1. Temos assim:
Escalas qualitativas – também designadas por escalas categóricas, cada observação é classificada numa das categorias.
Escalas nominais – as categorias não têm uma ordem natural ou, a ordem das categorias é arbitrária.
Exemplos destas escalas são a cor dos olhos ou o sexo de uma pessoa. Qualquer ordenamento das categorias é arbitrário, como, por exemplo, a ordem alfabética.
Escalas ordinais – as categorias têm uma ordem implícita ou existe um critério relevante para as ordenar.
Por exemplo, o clima de uma região (frio, ameno, quente) ou a satisfação com uma compra (muito insatisfeito, insatisfeito, indiferente, satisfeito, muito satisfeito). Nestes casos é possível estabelecer relações de ordem entre as categorias, podendo-se afirmar que frio < ameno < quente.
Escalas quantitativas – também designadas por escalas numéricas, em que as observações são expressas (e ordenadas) com um número.
Escalas de intervalo (ou relativas) – a origem (zero) da escala é arbitrária e não tem um significado especial. Nestas escalas, as diferenças são interpretáveis mas os rácios não o são.
O exemplo clássico é a temperatura expressa em graus centígrados (ou Celsius), em que a origem é definida arbitrariamente como o ponto de fusão da água. Ao comparar uma temperatura de 1 \(^\circ\)C com uma de 3 \(^\circ\)C, podemos afirmar que a segunda é maior e há uma diferença de 2 \(^\circ\)C. Não podemos afirmar que a segunda é o triplo da primeira porque a origem (0 \(^\circ\)C) não significa que não há temperatura (energia térmica).
Escalas absolutas (ou de rácio) – a origem é fixa e representa uma quantidade igual a zero.
Por exemplo, a idade de um indivíduo ou o número de irmãos. Em ambos os casos o zero significa nada. No exemplo da temperatura, caso aquela fosse medida na escala de Kelvin, uma temperatura igual a 0 \(^\circ\)K significa a ausência de energia térmica.
O facto de uma observação ser expressa num número não implica que se trate, necessariamente, de uma escala numérica. Por norma é, mas há exceções. Para que seja uma escala numérica, o número tem que representar uma quantidade. Por exemplo, o indicativo de um número de telefone (273, 276, …) é um número, mas está expresso numa escala nominal, uma vez que identifica uma região.
1.2.2 Natureza da medição
É também útil classificar as escalas numéricas quanto natureza da medição, expressa no conjunto de valores que as observações podem tomar. Assim, podemos ter:
- Dados discretos – a observação apenas poderá resultar num conjunto enumerável de valores (finito ou infinito).
O número de pontos obtido no lançamento de um dado pertence ao conjunto {1, 2, 3, 4, 5, 6} (finito). O número de irmãos de uma pessoa pertence ao conjunto \(\mathbb{N}\), ou seja {0, 1, 2, …}, podendo tomar valores arbitrariamente grandes.
- Dados contínuos – a observação pode tomar qualquer valor real (conjunto \(\mathbb{R}\)).
O peso de um indivíduo ou o tempo decorrido entre dois eventos podem tomar qualquer valor real e ser medidos com uma precisão, expressa num número de casas decimais, limitado apenas pelos instrumentos de medida e registo.
Na prática, todas as medições são discretas: é impossível medir a registar grandezas de forma absoluta (número infinito de casas decimais). No entanto, é muitas vezes mais prático tratar as observações como contínuas.
Frequentemente, as observações discretas resultam de contagens (número de …) e são expressas com números naturais. Já as observações contínuas resultam de medições instrumentais (peso, tempo, pressão, etc.) e são expressas com números reais e casas decimais.
Embora seja uma forma expedita de distinguir observações discretas de contínuas, trata-se de conceitos diferentes. Por exemplo, metade dos pontos no lançamento de um dado tem natureza discreta mas expressa-se com casas decimais.
1.2.3 Hierarquia das escalas
Os quatro tipos de escalas apresentados na secção Secção 1.2.1 foram ordenados de acordo com o seu grau de complexidade ou sofisticação. Esta complexidade advém do facto de, qualquer operação que se possa realizar numa determinada escala, pode ser realizada numa escala de nível hierárquico igual ou mais elevado. O contrário nem sempre é verdadeiro, depende da operação e das escalas em questão.
Por outro lado, qualquer medição feita numa determinada escala, pode ser convertida e expressa numa escala de nível hierárquico inferior.
Relembrando a ordem em relação à complexidade:
- Escala nominal.
- Escala ordinal.
- Escala de intervalo.
- Escala absoluta.
Para ilustrar o que foi dito, tome-se o exemplo já apresentado da temperatura. A temperatura pode ser medida na escala de Kelvin, uma escala absoluta. Podemos converter facilmente temperaturas Kelvin (\(K\)) para graus centígrados (\(C = K + 273.16\)). Note-se que esta conversão só se tornou trivial após uma série de avanços científicos.
Durante muito tempo foram utilizadas várias escalas de temperatura (Celsius, Fahrenheit e outras) pois ainda não se tinha desenvolvido o conceito de zero absoluto na termodinâmica. A escala de Kelvin apenas foi desenvolvida durante o século XIX, adotada pelo Sistema Internacional no século XX e definida com maior precisão, recentemente, em 2019.
Enquanto que na escala de Kelvin faz sentido dizer que um objeto com uma temperatura de 10 \(^\circ\)K contém o dobro da temperatura (energia térmica) do que o mesmo objeto com 5 \(^\circ\)K, quando as medições são feitas em graus centígrados (escala de intervalo), é incorreto afirmar que 10 \(^\circ\)C é o dobro da temperatura do mesmo objeto a 5 \(^\circ\)C, pois a origem da escala é arbitrária, ou seja, os rácios não têm significado em escalas de intervalo.
Podemos também converter facilmente temperaturas em graus centígrados para uma escala ordinal (designe-se por estado do tempo), fazendo corresponder, por exemplo:
- Se a temperatura for menor que 10 \(^\circ\)C, classificar como frio.
- Se a temperatura estiver entre 10 \(^\circ\)C e 20 \(^\circ\)C, classificar como ameno.
- Se a temperatura for superior a 20 \(^\circ\)C, classificar como quente.
Naturalmente, esta conversão tem pouco ou nenhum interesse, apenas se apresenta como exemplo ilustrativo.
Note-se que, sendo fácil converter uma temperatura para o estado do tempo, o contrário é impossível. Note-se também que as operações aritméticas que podiam ser utilizadas com temperaturas são agora impossíveis (embora haja um ou outro aluno, e não só, que acham o contrário).
Poder-se-ia também observar qual o algarismo das unidades das temperaturas e verificar se era par ou ímpar. Neste caso estar-se-ia a fazer uma conversão para uma escala nominal. Como é evidente, fazer a conversão inversa é impossível.
Na Figura 1.2 pode visualizar-se o exemplo apresentado.
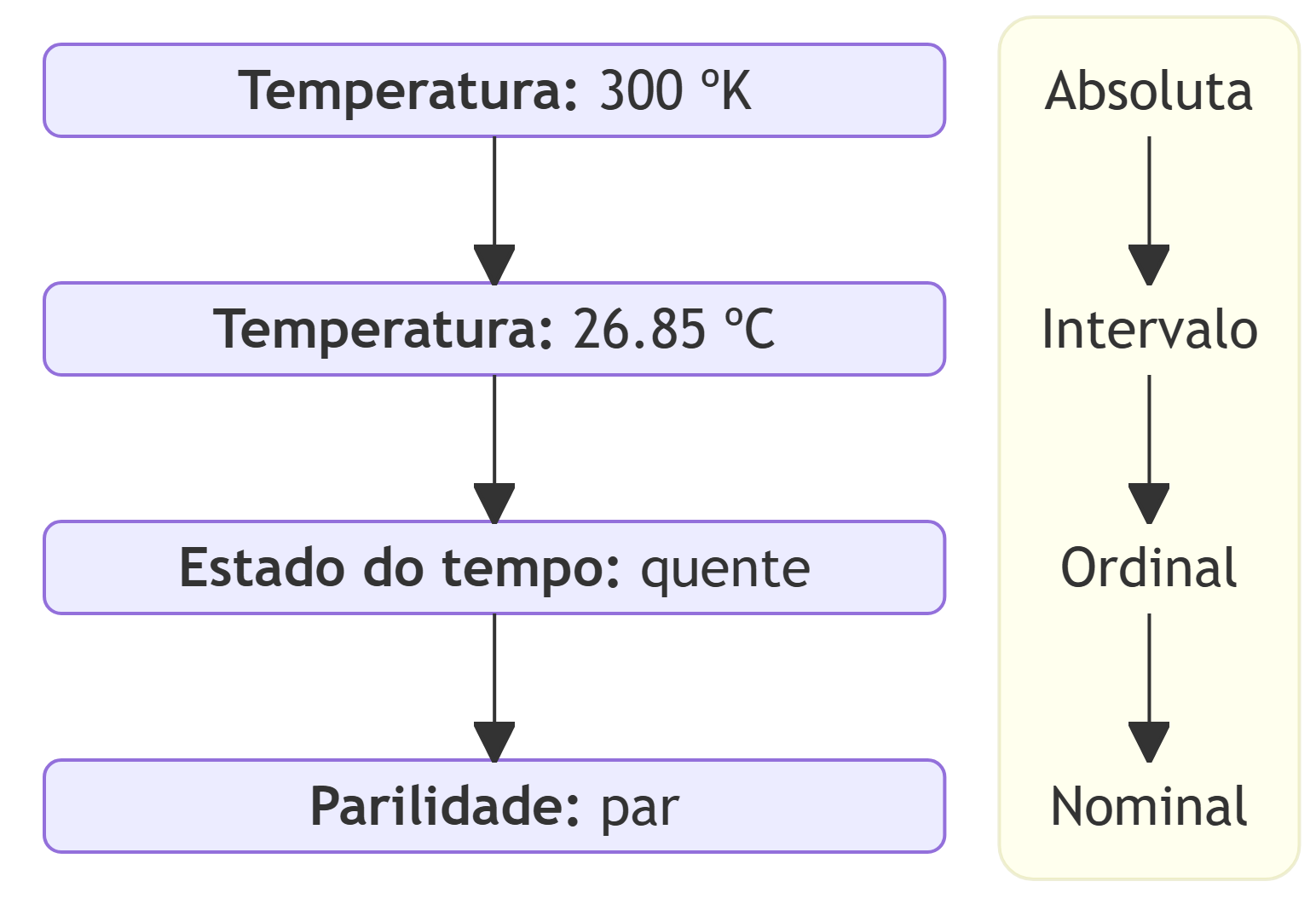
Geralmente, as conversões inversas são impossíveis, pois, na maior parte dos casos, não é possível estabelecer uma relação unívoca entre os valores, por falta de detalhe. Por exemplo, se souber que uma temperatura termina num algarismo par, não é possível saber, só com essa informação, qual o estado do tempo ou qual a temperatura na escala Celsius ou na escala Kelvin.
1.3 Organização dos dados
Para que a recolha de dados seja possível é necessário determinar quais as unidades estatísticas a observar (objetos, indivíduos, eventos, etc.) e quais as características que se vão observar ou medir para cada unidade.
Numa fase posterior, geralmente os dados são organizados num formato tabular ou matricial. A Tabela 1.1 mostra as primeiras linhas de um conjunto de dados popular (o dataset mtcars, incluído no R, que contém dados sobre diferentes características de vários modelos de carros).
mtcars
| mpg | cyl | disp | hp | drat | wt | qsec | vs | am | gear | carb | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mazda RX4 | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.620 | 16.46 | 0 | 1 | 4 | 4 |
| Mazda RX4 Wag | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.875 | 17.02 | 0 | 1 | 4 | 4 |
| Datsun 710 | 22.8 | 4 | 108.0 | 93 | 3.85 | 2.320 | 18.61 | 1 | 1 | 4 | 1 |
| Hornet 4 Drive | 21.4 | 6 | 258.0 | 110 | 3.08 | 3.215 | 19.44 | 1 | 0 | 3 | 1 |
| Hornet Sportabout | 18.7 | 8 | 360.0 | 175 | 3.15 | 3.440 | 17.02 | 0 | 0 | 3 | 2 |
| Valiant | 18.1 | 6 | 225.0 | 105 | 2.76 | 3.460 | 20.22 | 1 | 0 | 3 | 1 |
| Duster 360 | 14.3 | 8 | 360.0 | 245 | 3.21 | 3.570 | 15.84 | 0 | 0 | 3 | 4 |
| Merc 240D | 24.4 | 4 | 146.7 | 62 | 3.69 | 3.190 | 20.00 | 1 | 0 | 4 | 2 |
| Merc 230 | 22.8 | 4 | 140.8 | 95 | 3.92 | 3.150 | 22.90 | 1 | 0 | 4 | 2 |
| Merc 280 | 19.2 | 6 | 167.6 | 123 | 3.92 | 3.440 | 18.30 | 1 | 0 | 4 | 4 |
| Merc 280C | 17.8 | 6 | 167.6 | 123 | 3.92 | 3.440 | 18.90 | 1 | 0 | 4 | 4 |
| Merc 450SE | 16.4 | 8 | 275.8 | 180 | 3.07 | 4.070 | 17.40 | 0 | 0 | 3 | 3 |
| Merc 450SL | 17.3 | 8 | 275.8 | 180 | 3.07 | 3.730 | 17.60 | 0 | 0 | 3 | 3 |
| Merc 450SLC | 15.2 | 8 | 275.8 | 180 | 3.07 | 3.780 | 18.00 | 0 | 0 | 3 | 3 |
| Cadillac Fleetwood | 10.4 | 8 | 472.0 | 205 | 2.93 | 5.250 | 17.98 | 0 | 0 | 3 | 4 |
| Lincoln Continental | 10.4 | 8 | 460.0 | 215 | 3.00 | 5.424 | 17.82 | 0 | 0 | 3 | 4 |
| Chrysler Imperial | 14.7 | 8 | 440.0 | 230 | 3.23 | 5.345 | 17.42 | 0 | 0 | 3 | 4 |
| Fiat 128 | 32.4 | 4 | 78.7 | 66 | 4.08 | 2.200 | 19.47 | 1 | 1 | 4 | 1 |
| Honda Civic | 30.4 | 4 | 75.7 | 52 | 4.93 | 1.615 | 18.52 | 1 | 1 | 4 | 2 |
| Toyota Corolla | 33.9 | 4 | 71.1 | 65 | 4.22 | 1.835 | 19.90 | 1 | 1 | 4 | 1 |
| Toyota Corona | 21.5 | 4 | 120.1 | 97 | 3.70 | 2.465 | 20.01 | 1 | 0 | 3 | 1 |
| Dodge Challenger | 15.5 | 8 | 318.0 | 150 | 2.76 | 3.520 | 16.87 | 0 | 0 | 3 | 2 |
| AMC Javelin | 15.2 | 8 | 304.0 | 150 | 3.15 | 3.435 | 17.30 | 0 | 0 | 3 | 2 |
| Camaro Z28 | 13.3 | 8 | 350.0 | 245 | 3.73 | 3.840 | 15.41 | 0 | 0 | 3 | 4 |
| Pontiac Firebird | 19.2 | 8 | 400.0 | 175 | 3.08 | 3.845 | 17.05 | 0 | 0 | 3 | 2 |
| Fiat X1-9 | 27.3 | 4 | 79.0 | 66 | 4.08 | 1.935 | 18.90 | 1 | 1 | 4 | 1 |
| Porsche 914-2 | 26.0 | 4 | 120.3 | 91 | 4.43 | 2.140 | 16.70 | 0 | 1 | 5 | 2 |
| Lotus Europa | 30.4 | 4 | 95.1 | 113 | 3.77 | 1.513 | 16.90 | 1 | 1 | 5 | 2 |
| Ford Pantera L | 15.8 | 8 | 351.0 | 264 | 4.22 | 3.170 | 14.50 | 0 | 1 | 5 | 4 |
| Ferrari Dino | 19.7 | 6 | 145.0 | 175 | 3.62 | 2.770 | 15.50 | 0 | 1 | 5 | 6 |
| Maserati Bora | 15.0 | 8 | 301.0 | 335 | 3.54 | 3.570 | 14.60 | 0 | 1 | 5 | 8 |
| Volvo 142E | 21.4 | 4 | 121.0 | 109 | 4.11 | 2.780 | 18.60 | 1 | 1 | 4 | 2 |
Trata-se de uma organização lógica em que:
- cada coluna da tabela, geralmente designada por variável, contém os dados relativos a cada uma das características que foram observadas ao recolher os dados;
- cada linha da tabela, geralmente designada por observação ou caso, contém os dados relativos a cada uma das unidades estatísticas observadas.
Nestas tabelas, é frequente utilizar nomes de colunas curtos, por uma questão de comodidade na manipulação. No entanto, os dados devem ser acompanhados de uma descrição adequada de cada variável observada. Por exemplo, a variável mpg expressa o consumo de combustível de cada carro em milhas por galão americano. Na documentação do R encontram-se detalhadas as descrições de todas as variáveis.
Nestas tabelas, também é normal encontrar a informação codificada. Por exemplo, a variável am indica o tipo de transmissão do carro, tratando-se de uma variável nominal com 2 categorias: automática (0) e manual (1). Logo, embora a informação que aparece na tabela seja numérica, trata-se de códigos que correspondem a categorias nominais e as operações aritméticas com estes números, regra geral, não fazem sentido.
Tutoriais
Depois de ler este capítulo pode verificar como são implementados estes conceitos no ambiente computacional R. Os tutoriais listados abaixo estão diretamente relacionados com este capítulo.
| Tutorial | Descrição |
|---|---|
| Ferramentas | Instalação e configuração das ferramentas computacionais e dos fluxos de trabalho. |
| Introdução ao R | Noções básicas sobre manipulação de objetos, scripts, vetores, data frames e ficheiros de dados (CSV). |
| Dados no R | Estruturas de dados do R: vetores, matrizes, listas e data frames. Gravação e leitura de dados a partir de ficheiros. Especificação de variáveis qualitativas. |