|
CAPÍTULO 2: Encurvadura lateral de vigas |
Cap 2 - Instabilidade Lateral de Vigas.pdf |
Elementos
estruturais metálicos, como vigas, colunas ou treliças, são extensivamente
utilizados na construção metálica e na engenharia estrutural
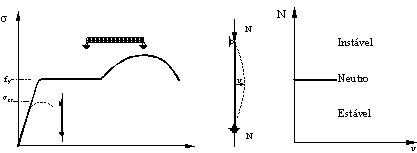
A estabilidade destes elementos estruturais envolve modos de colapso provocados pela perda de equilíbrio, em que uma pequena perturbação na força aplicada provoca um grande deslocamento, resultando num colapso estrutural, ver a Figura 2.1 . Os deslocamentos aumentam muito rapidamente e valores críticos são atingidos sob valores de carga crítica. Em aplicações práticas, a origem destas forças instabilizadoras pode estar na presença de imperfeições, porque nenhum elemento estrutural pode ser produzido idealmente. Para a definição do comportamento carga/deslocamento do elemento deve-se contabilizar o efeito da deformação através de uma teoria de segunda ordem, com referência à configuração de deformada do elemento, [2.2] .

Figura
2
.
1
– Comportamento à estabilidade, estados de equilíbrio.
Um grande número de elementos estruturais é considerado de parede fina, é esbelto e possui uma secção transversal aberta, considerando a baixos valores de rigidez à torção. É então importante que as cargas sejam aplicadas com uma baixa excentricidade relativamente ao centro de corte, diminuindo o efeito de torção. Se uma secção de parede fina é sujeita à torção, este estado é determinado por dois mecanismos, a rigidez à torção clássica de De Saint Vernant (1855) determinada pelo módulo de corte e pela contribuição do constrangimento ao empenamento da secção transversal associado à torção de St. Vernant. Se a variação do ângulo de torção é constante ao longo do elemento, o empenamento de todas as secções transversais é idêntico, pelo que a contribuição de segunda ordem desaparece. Este modo de torção é designado por torção homogénea. Quando existe uma variação, a torção designa-se de não homogénea, [2.3] [2.4] .
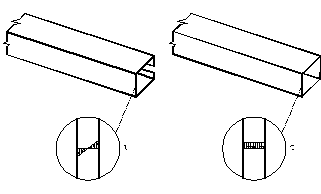
O empenamento da secção origina o aparecimento de tensões normais e tangenciais. A sua distribuição na espessura do elemento depende da geometria da secção transversal, em particular se é aberta ou fechada, ver a Figura 2.2 .
Figura
2
.
2
– Secção de parede fina, a) aberta, b) fechada.
Quando a secção
transversal é aberta, a tensão de corte devido à torção varia linearmente
a longo da espessura, com um valor nulo na superfície média. Vlassov
generalizou modelo cinemático de De Saint Vernant ao estudo da torção não
uniforme de secções abertas de parede fina. A teoria de Vlassov é baseada
na hipótese de a deformação de corte na superfície média ser nula. Este
pressuposto permite que o deslocamento axial
![]() seja proporcional à variação do
ângulo de torção
seja proporcional à variação do
ângulo de torção
![]() . O empenamento é dado por
. O empenamento é dado por
![]() , em que
, em que
![]() deixa de ser constante. A função
de empenamento,
deixa de ser constante. A função
de empenamento,
![]() , é definida por, [2.7]
;
, é definida por, [2.7]
;
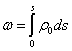 (2.1)
(2.1)
em
que
![]() é a distância na perpendicular
do centro de corte à tangente da linha média e
é a distância na perpendicular
do centro de corte à tangente da linha média e
![]() a distância do contorno da linha
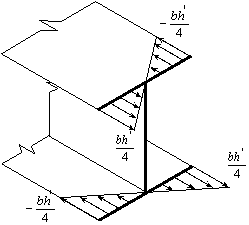
média da espessura, conforme a Figura 2.3
.
a distância do contorno da linha
média da espessura, conforme a Figura 2.3
.
|
|
|
|
a)
Elemento de parede fina monossimétrica |
b)
Função de empenamento de uma secção I. |
Figura
2
.
3
– Representação da função de empenamento.
A constante de empenamento da secção transversal é definida por,
![]() (2.2)
(2.2)
Quando a secção transversal é fechada, a tensão de corte não varia de sinal ao longo da espessura. A análise deve incluir as deformações de corte devido ao empenamento originado pela torção, [2.5] .
Além da baixa rigidez à torção, os elementos estruturais como vigas e colunas, possuem, em geral, baixa rigidez à flexão lateral. Este facto aliado à baixa rigidez à torção, leva a que possa ocorrer o colapso por instabilidade. Esta forma de instabilidade é designada por encurvadura lateral torsional.
Neste capítulo é apresentado, o modelo analítico de cálculo do momento crítico de vigas sujeitas à encurvadura lateral torsional, à temperatura ambiente. É apresentada ainda a verificação de segurança relativa a este estado limite último, de acordo com o Eurocódigo 3 Parte 1.1, [2.11] . É efectuada uma descrição da importância deste modo de instabilidade a elevadas temperaturas, e são apresentados os domínios de verificação da resistência em situação de incêndio, preconizados no Eurocódigo 3 Parte 1.2, [2.15] .